A small body of mass 500 g moves on a rough horizontal surface before finally stops. The initial velocity of the body is 2 m/s and coefficient of frictin is 0.3 Then, find absolute vlaue of the average pwoeer develped by the frictional force during the time of motion. (Take g=10m/s2)Solution in Telugu
1W
1.5W
2W
2.5W
The correct Answer is:B
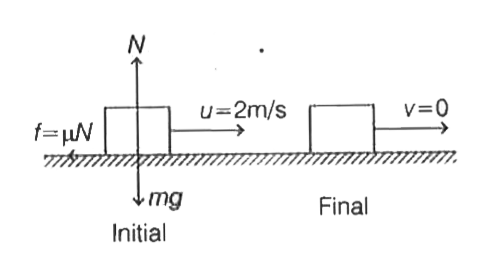
As, retardation is constant, so average velocity
vav=u+v2=2+02=1m/s
Now, friction force, f=μN=μmg
Given, coefficient of friction, μ=0.3
Mass of body, m=500g=0.5kg
⇒f=0.3×0.5×10
f=1.5N
Average power by friction,
Pav=fvav
Pav=1.5×1=1.5W
Similar Questions
A force of 500 dyn is applied against the motion of a body of mass 50 g moving at 1 m cdot s^(-1) . When and where will the body stop?
View Solution500 g द्रव्यमान का एक पिंड एक खुरदरे क्षैतिज मेज पर फिसलता है यदि पिण्ड तथा मेज के मध्य गुणांक 0.2 है तथा पिण्ड की प्रारम्भिक चाल60cm/s है । तब किया गया कार्य होगा
View Solution500 g द्रव्यमान का एक पिंड एक खुरदरे क्षैतिज मेज पर फिसलता है यदि पिण्ड तथा मेज के मध्य गुणांक 0.2 है तथा पिण्ड की प्रारम्भिक चाल60cm/s है । तब
पिण्ड को विरामावस्था में लाने के लिए घर्षण बल द्वारा किया गया कार्य
View Solution500 g द्रव्यमान का एक पिंड एक खुरदरे क्षैतिज मेज पर फिसलता है यदि पिण्ड तथा मेज के मध्य गुणांक 0.2 है तथा पिण्ड की प्रारम्भिक चाल60cm/s है । तब
वह समय इस पर यह रुकता है यदि t = 0 पर पिण्ड का वेग 60 cm/s है
View SolutionA body of mass 10 kg moves on rough horizontal surface with initial velocity 10m/s and travels 500m before coming to rest. The coefficient of friction is
View SolutionA small body of mass m moving with velocity v0 on rough horizontal surface, finally stops due to friction. Find, the mean power developed by the friction force during the motion of the body, if the frictional coefficient μ=0.27,m=1 kg and v0=1.5ms−1.
View SolutionThe velocity - time (V - t) graph of an object of mass 2 kg is as shown in figure while it is moving on a rough horizontal surface. The coefficient of friction between object and the surface is (g=10ms2)
View SolutionA body is projected with a initial velocity of (8hati+6hatj) m s^(-1) . The horizontal range is (g = 10 m s^(-2))
View Solution
