समान द्रव्यमान m के तीन बिंदु द्रव्यमान l भुजा वाले एक समबाहु त्रिभुज के शीर्ष पर स्थित हैं । इसके केंद्र ( Centroid ) पर गुरुत्वीय क्षेत्र एवं विभव का मान ज्ञात कीजिए ।
Video Solution
Text Solution
चित्र में ABC एक समबाहु Δ है ।
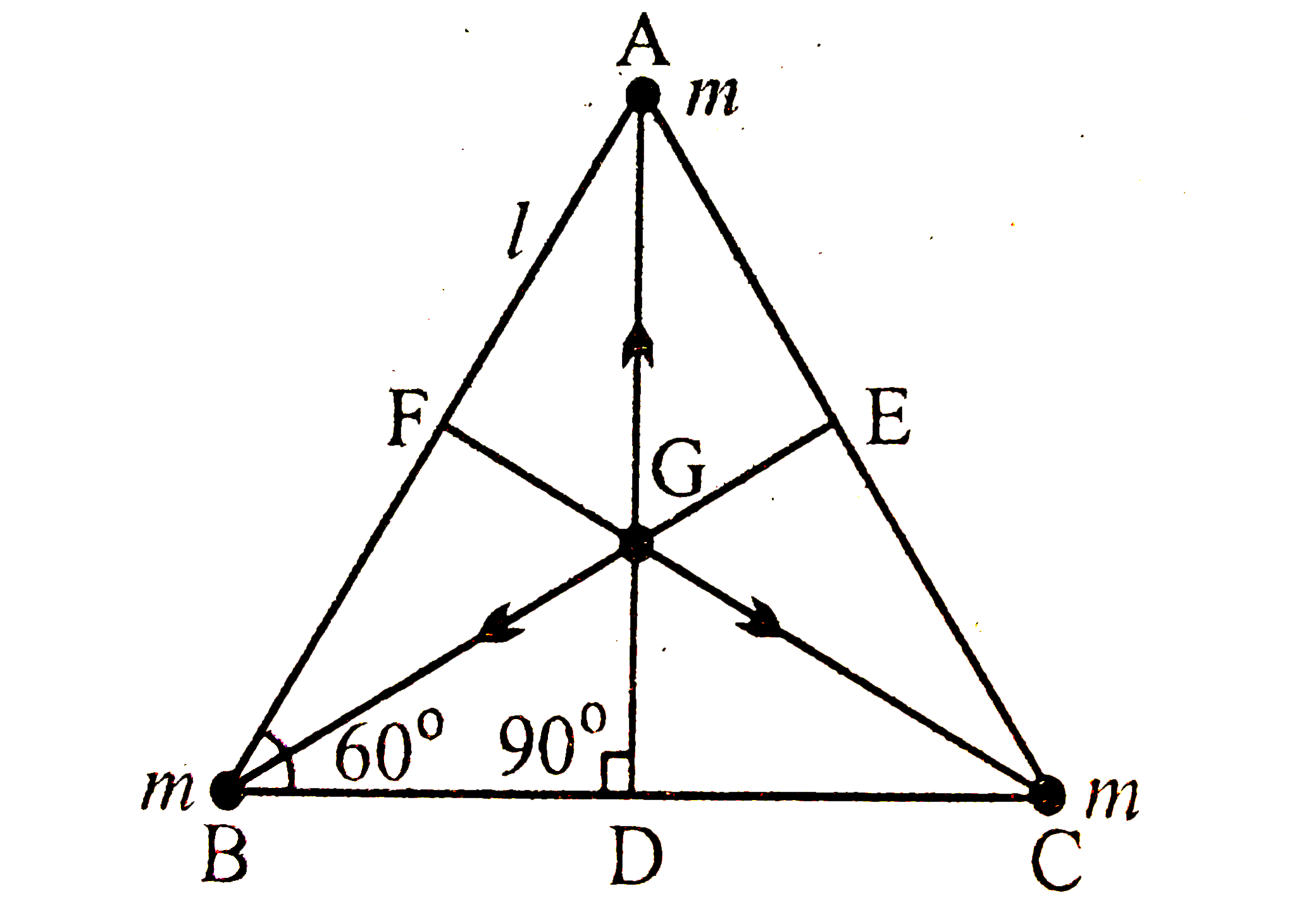
G उसका केंद्र है।
समकोण ΔADB में,
sin60∘=ADAB⇒√32=ADl⇒AD=√3l2
किन्तु AG=23ADrARrAG=23×√3l2=l√3
इसी तरह BG=1√3 तथा CG=l√3
अतः AG=BG=CG=l√3
बिंदु A पर स्थित बिंदु द्रव्यमान m के कारण G पर गुरुत्वीय क्षेत्र EA=GmAG2
बिंदु B पर स्थित बिंदु द्रव्यमान m के कारण G पर गुरुत्वीय क्षेत्र EB=GmBG2
बिंदु C पर स्थित बिंदु द्रव्यमान m के कारण G पर गुरुत्वीय क्षेत्र EC=GmCG2
अतः EA=EB=EC=E (मानलो)
तीनों बलों के बीच का परिणामी का परिमाण तीसरे बल के परिमाण के बराबर है।
अतः केंद्र G पर गुरुत्वीय क्षेत्र का मान शून्य होगा। अब बिंदु पर गुरुत्वीय विभव
=−GmAG+(−GmBG)+(−GMCG)
=−GM[1AG+1BG+1CG]
=−GM[√3l+√3l+√3l]
=−3√3GMl.
|
Similar Questions
1 किग्रा, (32) किग्रा, एवं 2 किग्रा द्रव्यमानों के तीन कण a भुजा वाले एक समबाहु त्रिभुज के शीर्षों पर रखे गये हैं। द्रव्यमान केन्द्र के X, Y निर्देशांक होंगे-
View Solutionवलय के अक्ष पर स्थित बिंदु पर विधुत क्षेत्र की तीव्रता
View Solutionवृत्ताकार पथ पर आवेश की गति के कारण केंद्र पर चुंबकीय क्षेत्र|धारावाहि चाप के कारण केंद्र पर चुंबकीय क्षेत्र
View Solutionगुरुत्वाकर्षण|गुरुत्वीय क्षेत्र #!#दो द्रव्यमान कणों के निकाय की गुरुत्वीय स्थितिज उर्जा
View Solutionद्रव्यमान केंद्र पर महत्वपूर्ण उधारण
View Solutionn कणों के निकाय के द्रव्यमान का केंद्र#!#अभ्यास प्रश्न
View Solutionद्रव्यमान केंद्र|विविक्त कणों के निकाय का द्रव्यमान केंद्र|विभिन्न कणों के निकाय का द्रव्यमान केंद्र|सतत वितरण वाले द्रव्यमान का द्रव्यमान केंद्र|द्रव्यमान केंद्र की गति|OMR|Summary
View Solutionद्रव्यमान केंद्र |विवित्तक कणो के नियम के लिए द्रव्यमान केंद्र |OMR
View Solution

