In the system shown in figure, mass m is released from rest from position A. Suppose potential energy of m at point A with respect to point B is E. Volume of m is negligible and all surfaces are smooth. When mass m reaches at point B
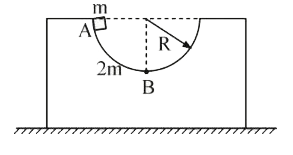
column IcolumnII(A)Kinetic Energy of m(P)E/3(B)Kinetic Energy of 2m (Q)2E/3(C)Momentum of m(R)√43mE(D)Momentum of 2m(S)√23mE(T)None
The correct Answer is:A – Q; B – P; C – R; D – R
Given: mgR = E
When m reaches point B:
Applying momentum conservation in horizontal: 0=mv1+2m(−v2)⇒v1=2v2
Applying energy conservation:
−mgR+0+(12mv21−0)+(122mv22−0)=0,12m(2v2)2+122mv22=mgR.
⇒3mv22=mgR⇒v2=√gR3,v1=2v2=2√gR3
K.E.ofm=12mv21=12m⎛⎝2√gR3⎞⎠2=23mgR=2E3
K.Eof2m=122mv22=122m⎛⎝√gR3⎞⎠2=mgR3=E3
Momentum of m=mv1=m2√gR3=√43mE, Momentum of 2m=2V2=2m√gR3=√43ME
Similar Questions
In the system shown in figure, mass m is released from rest from position A. Potential energy of m at point A with respect to point B is E. Volume of m is negligible and all surfaces are smooth. When mass m reaches at point B.
View SolutionIn the system shown in figure, mass m is released from rest from position A. Suppose potential energy of m at point A with respect to point B is E. Dimensions of m negligible and all surfaces are smooth. When mass reaches at point B.

View Solution
Knowledge Check
A charged particle of mass m and charge e is released from rest in an electric field E. If kinetic energy of particle after time t is Ek and linear momentum is p, then
Ap=EetBp=2eEtCEK=e2E2t22mDEK=e2E2t2mA charged particle of mass m and charge q is released from rest in an electric field of constant magnitude E. The kinetic energy of the particle after time t is
A2E2t2mqBE2q2r22mCEq2m2t2DEqm2tA charged particle of mass m and charge q is released from rest in an electric field of constant magnitude E. The kinetic energy of the particle after time t is
A2E2t2mqBE2q2t22mCEq2m2t2DEqm2t
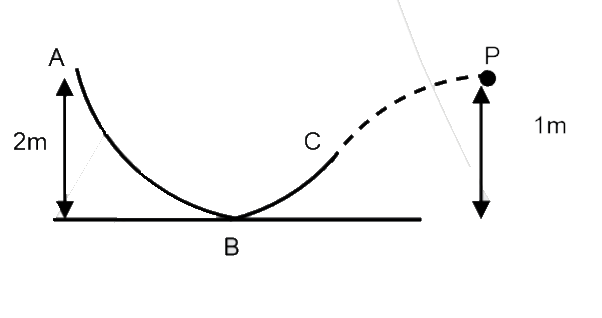
A particle is released at point A. Find Kinetic energy at point P Given m = 1 kg and all surfaces are frictionless
View SolutionA particle is released from rest at origin.It moves under influence of potential energy U=(x2−3x) ,the kinetic energy at x=2m is
View SolutionA particle of mass m, kinetic energy K and momentum p collision head on elastically with another particle of mass 2m at rest. After collision. :
Column IColumn II(A)Momentum of first particle(p)3/4p(B)Momentum of second particle(q)−K/9(C)Kinetic energy of first particle(r)−p/3(D)Kinetic energy of second particle(s)8K9None
View SolutionA particle A of mass m is situated at highest point of wedge B of mass 2m is released from rest. Then distance travelled by wedge B( with respect to ground ) when particle A reaches at lowest position. Assume all surfaces are smooth.

View SolutionA charged particle of mass m and charge e is released from rest in an electric field of constant magnitude E. The kinetic energy of the particle after time t is Ek and the linear momentum is p. We have
View Solution

