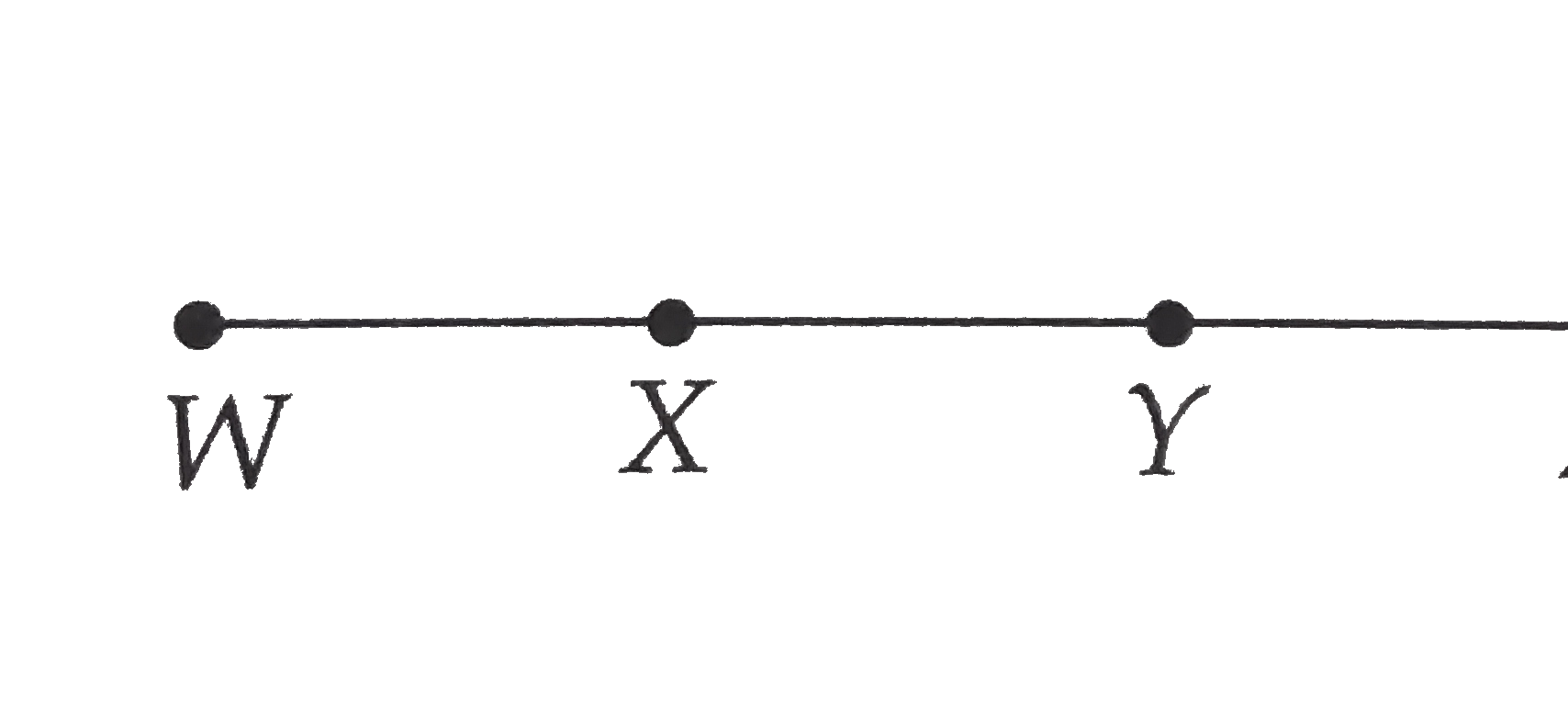
The points P,Q,R and S lie in that order on a straight line . The midpoint of ¯¯¯¯¯¯QS is R and the midpoint of ¯¯¯¯¯PS is Q . The length of ¯¯¯¯¯¯QR is x feet and the length of ¯¯¯¯¯¯PQ is 4x−16 feet . What is the length , in feet , of ¯¯¯¯¯PS?
32
20
16
8
The correct Answer is:A
To solve the problem, we will follow these steps:
Step 1: Understand the relationships between the points
We know that:
- Points P, Q, R, and S lie on a straight line in that order.
- R is the midpoint of segment QS.
- Q is the midpoint of segment PS.
- The length of segment QR is x feet.
- The length of segment PQ is 4x−16 feet.
Step 2: Establish the lengths of segments based on midpoints
Since R is the midpoint of QS, we have:
- QR=x
- RS=x
Thus, the total length of segment QS is:
QS=QR+RS=x+x=2x
Since Q is the midpoint of PS, we have:
- PQ=4x−16
And since Q is the midpoint of PS:
PQ=QS
This gives us the equation:
4x−16=2x
Step 3: Solve the equation for x
Now, we will solve the equation:
4x−16=2x
Subtract 2x from both sides:
4x−2x−16=0
2x−16=0
Add 16 to both sides:
2x=16
Now, divide by 2:
x=8
Step 4: Find the length of segment PS
Now that we have x, we can find the length of PS. The length of PS can be calculated as:
PS=PQ+QR+RS
Substituting the known lengths:
- PQ=4x−16
- QR=x
- RS=x
So,
PS=(4x−16)+x+x
PS=4x−16+2x
PS=6x−16
Now substitute x=8:
PS=6(8)−16
PS=48−16
PS=32
Final Answer
The length of segment PS is 32 feet.
---
We know that:
- Points P, Q, R, and S lie on a straight line in that order.
- R is the midpoint of segment QS.
- Q is the midpoint of segment PS.
- The length of segment QR is x feet.
- The length of segment PQ is 4x−16 feet.
Since R is the midpoint of QS, we have:
- QR=x
- RS=x
QS=QR+RS=x+x=2x
- PQ=4x−16
PQ=QS
This gives us the equation:
4x−16=2x
Now, we will solve the equation:
4x−16=2x
4x−2x−16=0
2x−16=0
2x=16
x=8
Now that we have x, we can find the length of PS. The length of PS can be calculated as:
PS=PQ+QR+RS
- PQ=4x−16
- QR=x
- RS=x
PS=(4x−16)+x+x
PS=4x−16+2x
PS=6x−16
PS=6(8)−16
PS=48−16
PS=32
The length of segment PS is 32 feet.
Topper's Solved these Questions
Similar Questions
Knowledge Check

What is the length of ¯¯¯¯¯¯QR ?A5B5√22C10√2D5√2In the figure below, ABCD is a rectangle, EFGH is a square, and ¯¯¯¯¯¯CD is a diameter of a semicircle. Point K is the midpoint of ¯¯¯¯¯¯CD. Point J is the midpoint of both ¯¯¯¯¯¯AB and ¯¯¯¯¯¯EF. Points E and F lie on ¯¯¯¯¯¯AB. The 3 given lengths are in meters.
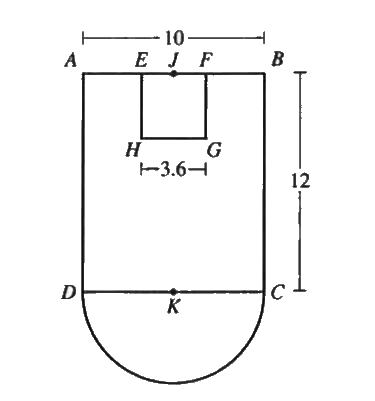
What is the length, in meters, of ¯¯¯¯¯¯JD?A13B15.6C17D√44In the figure below, ABCD is a rectangle, EFGH is a square, and ¯¯¯¯¯¯CD is a diameter of a semicircle. Point K is the midpoint of ¯¯¯¯¯¯CD. Point J is the midpoint of both ¯¯¯¯¯¯AB and ¯¯¯¯¯¯EF. Points E and F lie on ¯¯¯¯¯¯AB. The 3 given lengths are in meters.
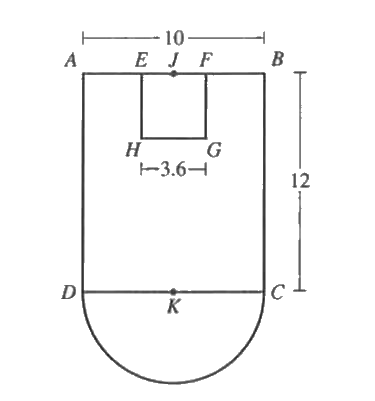
What is the length, in meters, of are ¯¯¯¯¯¯CD?A2.5πB5πC6.25πD10π
Magnetic length of a bar magnet is
View SolutionIn the figure below, ABCD is a rectangle, EFGH is a square, and ¯¯¯¯¯¯CD is a diameter of a semicircle. Point K is the midpoint of ¯¯¯¯¯¯CD. Point J is the midpoint of both ¯¯¯¯¯¯AB and ¯¯¯¯¯¯EF. Points E and F lie on ¯¯¯¯¯¯AB. The 3 given lengths are in meters.
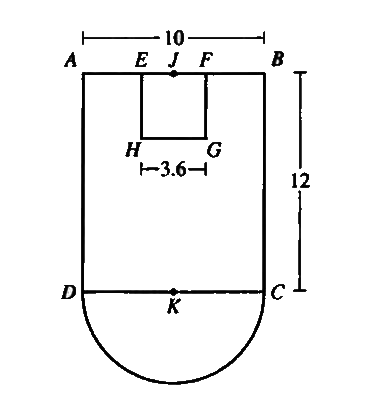
The length of ¯¯¯¯¯¯EH is what precent of the length of ¯¯¯¯¯¯AD?
View SolutionPoint C ( 1,2) and point D ( 7,10) lie in the standard coordiant plane . What are the coordinates of the midpoints of ¯¯¯¯¯¯CD
View SolutionIn isosceles triangle ABC below , the measures of ∠BAC and ∠BCA are equal and ¯¯¯¯¯¯DE∣∣¯¯¯¯¯¯AC.The diagonals of trapeziod DECA intersect at F . The length of ¯¯¯¯¯¯DE is 9 centimeters , and the length of ¯¯¯¯¯¯AC is 27 centimeters . what is the length , in centimeters , of ¯¯¯¯¯¯FC ?

View SolutionPoint A, B, and C all lie on a line. Point D is midpoint of ¯¯¯¯¯¯AB and E is the midpoint of BC,¯¯¯¯¯¯AB=4and¯¯¯¯¯¯BC=10. Which of the following could be the length of ¯¯¯¯¯¯AE?
View Solution