The geometric mean of 3 positive numbers is the cube root of the product of the 3 numbers. What is the geometric mean of 2,4 and 27 ?
6
11
21
72
The correct Answer is:A
Topper's Solved these Questions
Similar Questions
If Alex can fold 12 napkins in x minutes, how many napkins can be fold in y hours?
View SolutionFor each of 3 years , the table below gives the number of different routes a runner ran , the number of runs she ran , and the total number of miles she ran .
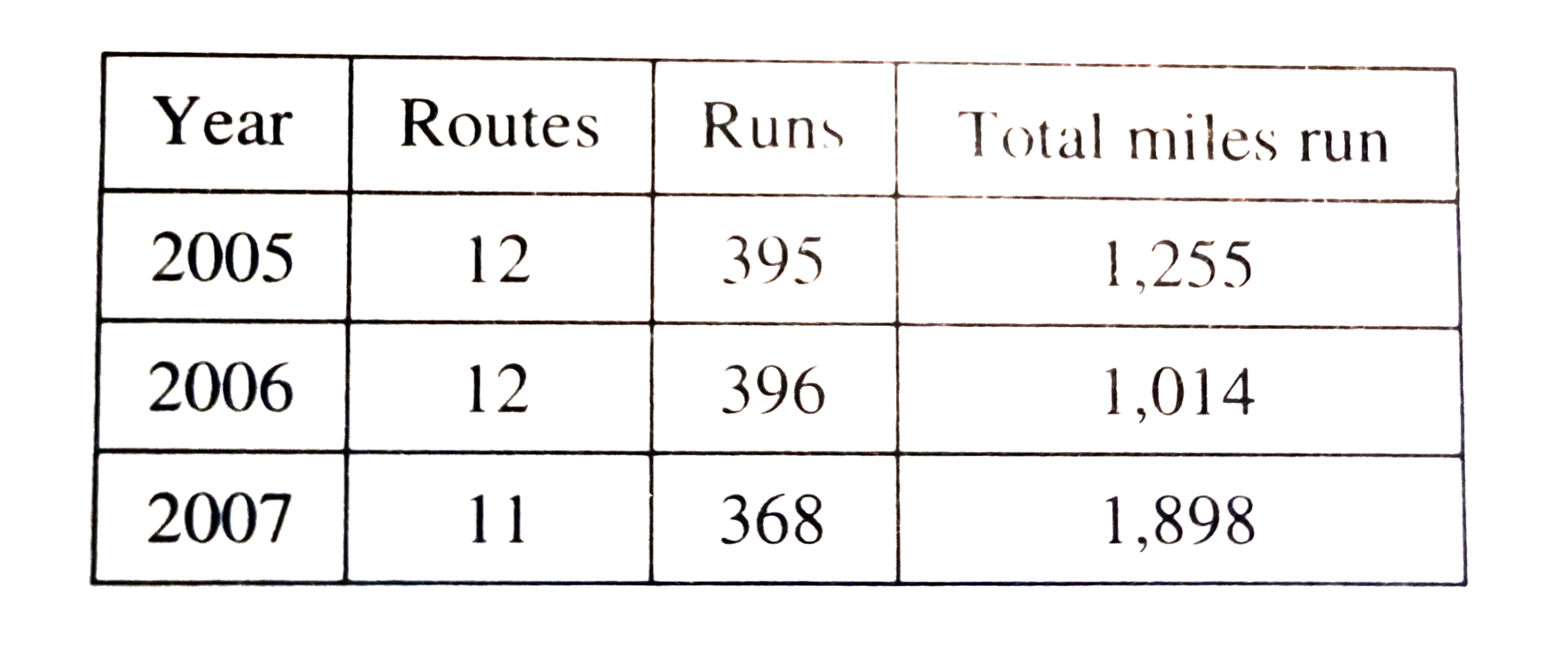
To the nearest tenth of a mile , what is the average number of miles the runner ran per run in 2005 ?
View SolutionIf the AM of two positive numbers be three times their geometric mean then the ratio of the numbers is
View SolutionThe ratio of geometric and arithmetic mean of two real numbers is 3:5. Then find the ratio of their harmonic mean and geometric mean.
View SolutionIf the ratio of the arithmatic mean and the geometric mean of two positive numbers is 3:2, then find the ratio of the geometric mean and the harmonic mean of the numbers.
View SolutionGeometric mean of 3, 9 and 27, is
View SolutionThe arithmetic mean of two numbers exceeds their geometric mean by 2 and the geometric mean exceeds their harmonic mean by 1.6. What are the two numbers ?
View SolutionIf a is a positive number such that the arithmatic mean of a and 2 exceeds their geometric mean by 1. Then, the value of a is
View Solutionयदि दो धनात्मक संख्याओं a और b के AM (समान्तर माध्य ) से GM (गुणोत्तर माध्य ) का अनुपात 5:3 है, तो a:b किसके बराबर है ?
View SolutionColumn AThe arithmetic mean (average) of the number a and b is 17. The geometric mean of the numbers a and b is 8. The geometric mean of two numbers is defined to be the square root of their productColumn Bab
View Solutionमाना कि दो संख्याओं का समान्तर माध्य 9 तथा गुणोत्तर माध्य 4 है । तब यह संख्याएँ निम्नलिखित द्विघात समीकरण के मूल हैं :
View SolutionThe geometric mean of the numbers 3, 9, 27, 81, 243 is :
View SolutionFind the Geometric mean of 3, 9, 27.
View SolutionThe arithrmetic mean of two positive numbers is 9 and geometric mean is 4. Then these numbers are the roots of the equation
View SolutionThe harmonic mean of two numbers is 4. Their arithmetic mean A and the geometric mean A and the geometric mean G satisfy the relation 2A+G2=27 . Find the numbers.
View Solution

