During their daily training race, Carl has to stop to tie his shoes . Melissa, whose shoes are Velcro , continues to run and gets 20 feet ahead of Carl . Melissa is running at a constant rate of 8 feet per second , and Carl starts running at a constant rate of 9.2 feet per second to catch up to Melissa . Which of the following equations , when solved for s, gives the number of seconds Carl will take to catch up to Melissa ?
8s+20=9.2s
8s-20=9.2s
20+9.2s9.2=8s
8s=20
The correct Answer is:A
To solve the problem of how long it will take Carl to catch up to Melissa, we can use the distance formula, which states that distance (D) is equal to rate (R) multiplied by time (T).
1. Identify the Variables:
- Let s be the time in seconds that Carl takes to catch up to Melissa.
- Melissa's speed is 8 feet per second.
- Carl's speed is 9.2 feet per second.
- Melissa has a 20-foot head start.
2. Write the Distance Formula for Both Runners:
- The distance Carl runs in time s is given by:
DC=Rate of Carl×Time=9.2s
- The distance Melissa runs in the same time s plus her head start is:
DM=Rate of Melissa×Time+Head Start=8s+20
3. Set the Distances Equal:
- Since both distances are equal when Carl catches up to Melissa, we can set the two equations equal to each other:
9.2s=8s+20
4. Rearrange the Equation:
- To isolate s, we can subtract 8s from both sides:
9.2s−8s=20
- This simplifies to:
1.2s=20
5. Solve for s:
- Now, divide both sides by 1.2 to find s:
s=201.2
6. Final Equation:
- The equation we derived from the problem that gives the time s is:
8s+20=9.2s
Conclusion:
The correct equation that gives the number of seconds Carl will take to catch up to Melissa is:
8s+20=9.2s
- Let s be the time in seconds that Carl takes to catch up to Melissa.
- Melissa's speed is 8 feet per second.
- Carl's speed is 9.2 feet per second.
- Melissa has a 20-foot head start.
- The distance Carl runs in time s is given by:
DC=Rate of Carl×Time=9.2s
- The distance Melissa runs in the same time s plus her head start is:
DM=Rate of Melissa×Time+Head Start=8s+20
- Since both distances are equal when Carl catches up to Melissa, we can set the two equations equal to each other:
9.2s=8s+20
- To isolate s, we can subtract 8s from both sides:
9.2s−8s=20
- This simplifies to:
1.2s=20
- Now, divide both sides by 1.2 to find s:
s=201.2
- The equation we derived from the problem that gives the time s is:
8s+20=9.2s
The correct equation that gives the number of seconds Carl will take to catch up to Melissa is:
8s+20=9.2s
Topper's Solved these Questions
Similar Questions
Two runners in a 100-m race start from the same place. Runner A starts as soon as the starting gun is fired and runs at a constant speed of 8.00 m/s Runner B starts 2.00 s later and runs at a constant speed of 10 m/s :-
View SolutionIn the figure below, a highway rest area (at D) and radar stations (at A and B) lie on a level east-west line, A is 9,000 feet due west of D. An airplane (at C) is shown directly above the rest area, flying due west at a constant speed of 300 feet per secod and at a constant altitude of 12,000 feet. The airplane is located at a straight-line distance of 15,000 feet from the radar station at A and 13,000 feet from the radar station at B.
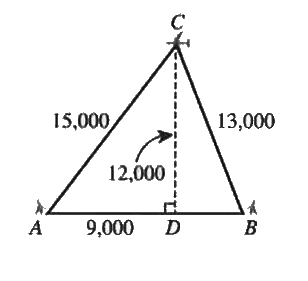
Which of the following values is closest to the number of seconds it will take for the airplane to fly from C to the point directly above the radar station at A?
View Solution
Knowledge Check
The front of a roller-coaster car is at the bottom of a hill and is 15 feet above the ground. If the front of the roller-coaster car rises at a constant rate of 8 feet per second, which of the following equations gives the height h, in feet, of the front of the roller-coaster car s seconds after it starts up the hill?
Ah = 8s + 15Bh=15s+3358Ch=8s+33515Dh = 15s + 8The length of a rectangular banner is 3 feet 2 inches, and the width is 2 feet 4 inches. Which one of the following equals the area of the banner?
A5 sq. feetB5 1/2 sq. feetC6 1/3 sq. feetD7 7/18 sq. feetA helicopter, initially hovering 40 feet above the ground, begins to gain altitude at a rate of 21 feet per second. Which of the following functions represents the helicopter’s altitude above the ground y, in feet, t seconds after the helicopter begins to gain altitude?
Ay = 40 + 21By = 40 + 21tCy = 40 − 21tDy = 40t + 21
h=−16t2+vt+k
The equation above gives the height h, in feet, of a ball t seconds after it is thrown straight up with an initial speed of v feet per second from a height of k feet. Which of the following gives v in terms of h, t, and k ?
View SolutionStudent studying motion observed a cart rolling at a constant rate along a striaght line. The table below gives the distance, d feet, the cart was from a reference point at 1-second intervals from t = 0 seconds to r = 5 seconds.
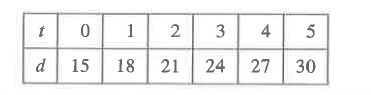
Which of the following equations represents this relationship between d and t?
View SolutionNicky and Cristina begin running a race at the same time, though Nicky begins the race at the same time, though Nicky begins the race 36 meters ahead of Cristina. If Cristina runs at a pace of 5 meters per second and Nicky runs at a pace of only 3 meters per second, how many seconds will Nicky have run before Cristina catches up to him?
View SolutionThe area of the base of a tank is 100 sq. ft. It takes 20 second to fill the tank with water poured at rate of 25 cubic feet per second. What is the height in feet of the rectangluar tank?
View SolutionThe distance, d, an acceleration rate, in meters per second per second. If a car accelerates from a stop at the rate of 20 meters per second per second and travels a distance of 80 meters, about how many seconds did the car travel?
View Solution

