Assuming that half the population are consumers of chocolate, so that the chance of an individual being a consumer is 1/2, and assuming that 100 investigators each take ten individuals to see whether they are consumers, how many investigators would you expect to report that 3 people or less were consumers?
To solve the problem, we need to determine how many investigators would report that 3 or fewer individuals are consumers of chocolate. We will use the binomial distribution formula for this calculation.
1. Define the Parameters:
- Probability of an individual being a consumer of chocolate, p=12.
- Probability of an individual not being a consumer, q=1−p=12.
- Number of individuals sampled by each investigator, n=10.
- Number of investigators, N=100.
2. Calculate the Probability for 0, 1, 2, and 3 Consumers:
We will calculate the probability of having 0, 1, 2, and 3 consumers using the binomial probability formula:
P(X=k)=(nk)pkqn−k
where k is the number of consumers.
- For 0 consumers (k=0):
P(X=0)=(100)(12)0(12)10=1⋅1⋅11024=11024
- For 1 consumer (k=1):
P(X=1)=(101)(12)1(12)9=10⋅12⋅1512=101024
- For 2 consumers (k=2):
P(X=2)=(102)(12)2(12)8=45⋅14⋅1256=451024
- For 3 consumers (k=3):
P(X=3)=(103)(12)3(12)7=120⋅18⋅1128=1201024
3. Sum the Probabilities:
Now we will sum the probabilities of having 0, 1, 2, or 3 consumers:
P(X≤3)=P(X=0)+P(X=1)+P(X=2)+P(X=3)
P(X≤3)=11024+101024+451024+1201024=1761024
4. Calculate the Expected Number of Investigators:
To find the expected number of investigators who report 3 or fewer consumers, multiply the total number of investigators by the probability:
Expected Investigators=N⋅P(X≤3)=100⋅1761024
=176001024=27516≈17.1875
Thus, the expected number of investigators who would report that 3 or fewer individuals were consumers is approximately 17.
- Probability of an individual being a consumer of chocolate, p=12.
- Probability of an individual not being a consumer, q=1−p=12.
- Number of individuals sampled by each investigator, n=10.
- Number of investigators, N=100.
We will calculate the probability of having 0, 1, 2, and 3 consumers using the binomial probability formula:
P(X=k)=(nk)pkqn−k
where k is the number of consumers.
P(X=0)=(100)(12)0(12)10=1⋅1⋅11024=11024
P(X=1)=(101)(12)1(12)9=10⋅12⋅1512=101024
P(X=2)=(102)(12)2(12)8=45⋅14⋅1256=451024
P(X=3)=(103)(12)3(12)7=120⋅18⋅1128=1201024
Now we will sum the probabilities of having 0, 1, 2, or 3 consumers:
P(X≤3)=P(X=0)+P(X=1)+P(X=2)+P(X=3)
P(X≤3)=11024+101024+451024+1201024=1761024
To find the expected number of investigators who report 3 or fewer consumers, multiply the total number of investigators by the probability:
Expected Investigators=N⋅P(X≤3)=100⋅1761024
=176001024=27516≈17.1875
Similar Questions
How many ATPs are consumed in HMS?
View Solutionসমগ্রকের অর্ধাংশ নিরামিষভোজী হওয়ার সম্ভাবনা 1/2 হয়, নিরামিষভোজী কিনা তা জানার জন্য 100 জন অনুসন্ধানকারীরপ্রত্যেকে 10 জন সদস্যের একটি করে নমুনা গ্রহণ করে। কতজন অনুসন্ধানকারীর 3 জন বা তার কম সংখ্যক ব্যক্তি নিরামিষভোজী হওয়ার পক্ষে রিপোর্ট দাখিল করবে বলে তুমি মনে করো।
View SolutionHow many chocolates will a consumer have, , if they are available free of cost?
View Solutionनिम्नांकित में से किसे आप ‘उपभोक्ता’ की श्रेणी में रखेंगे ?
View SolutionAssuming that half the population are consumers of chocolate, so that the chance of an individual being a consumer is 1/2, and assuming that 100 investigators each take ten individuals to see whether they are consumers, how many investigators would you expect to report that 3 people or less were consumers?
View SolutionIf three loaves of bread are consumed by 9 people, how many people will consume 9 loaves of bread?
View SolutionThe given diagram represents the relationships between organisms in a remote pond ecosystem. From this information. Which of the following is the most likely to be correct?
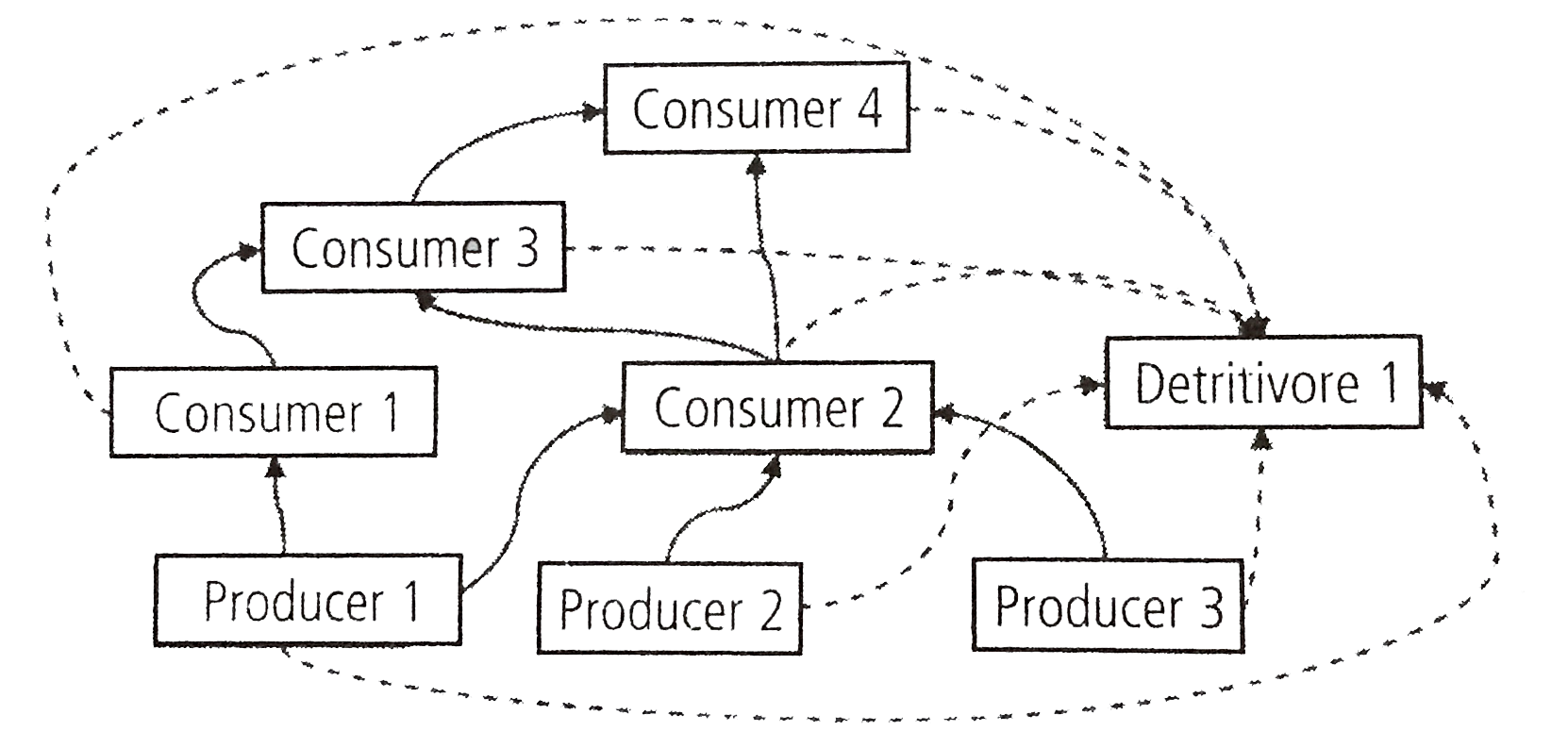
1) DDT present in the ecosystem would accumulate to the highest concentrations in the tissues of detritivore 1.
2) The introduction of consumer 4 individuals from an external population would lead a temporary increase in number of producer 2.
3) Disease in the producer 1 population would lead to an increase in the producer 3 population.
4) Extermination of consumer 3 would cause a sustained increase in the population of consumer 2.
View SolutionDwarfness is desired in ______________ , so that less nutrients are consumed by these crops.
View Solution

