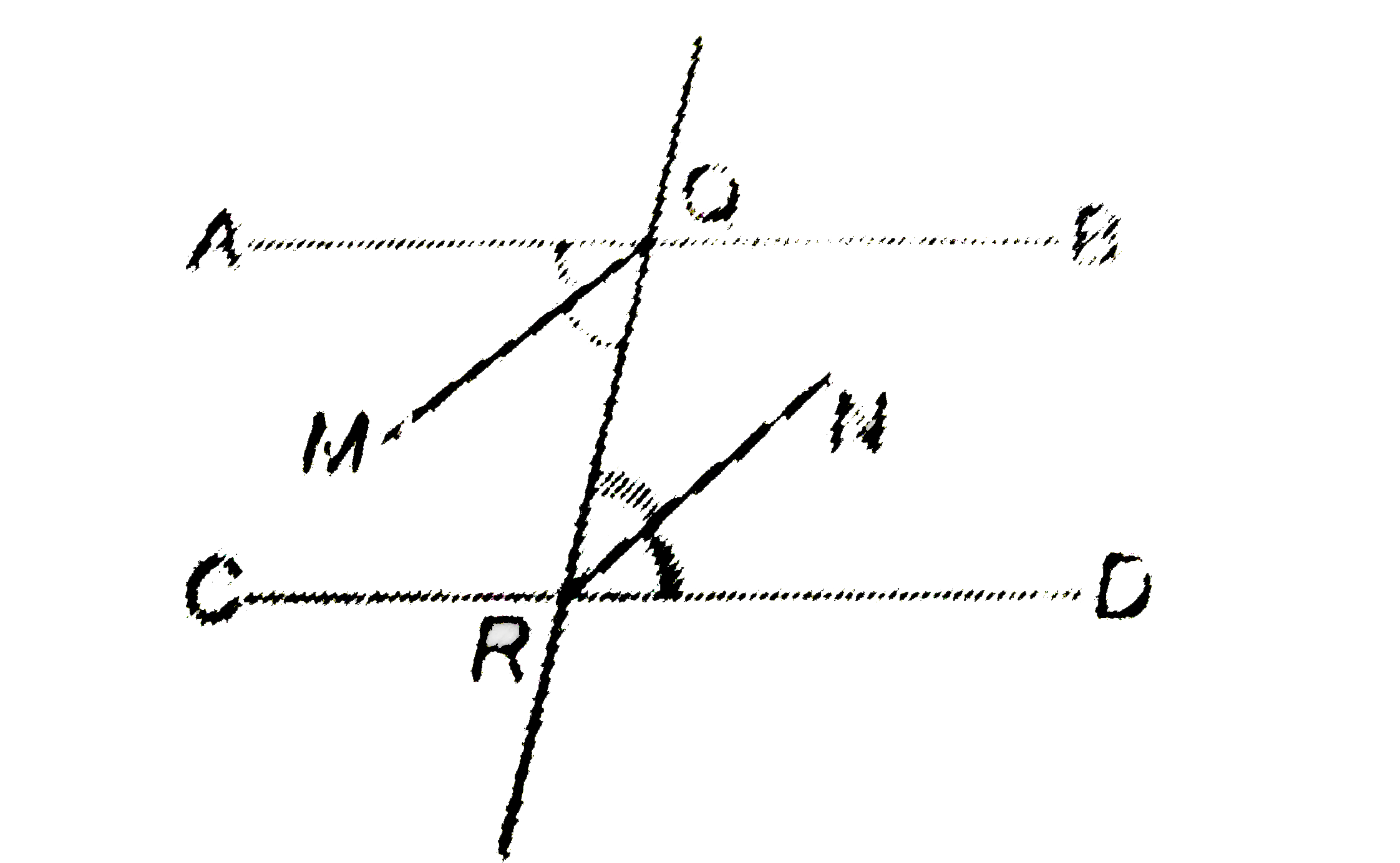
In the given figure, bisectors AP and BQ of the alternate interior angles are parallel, then show that l ||m.
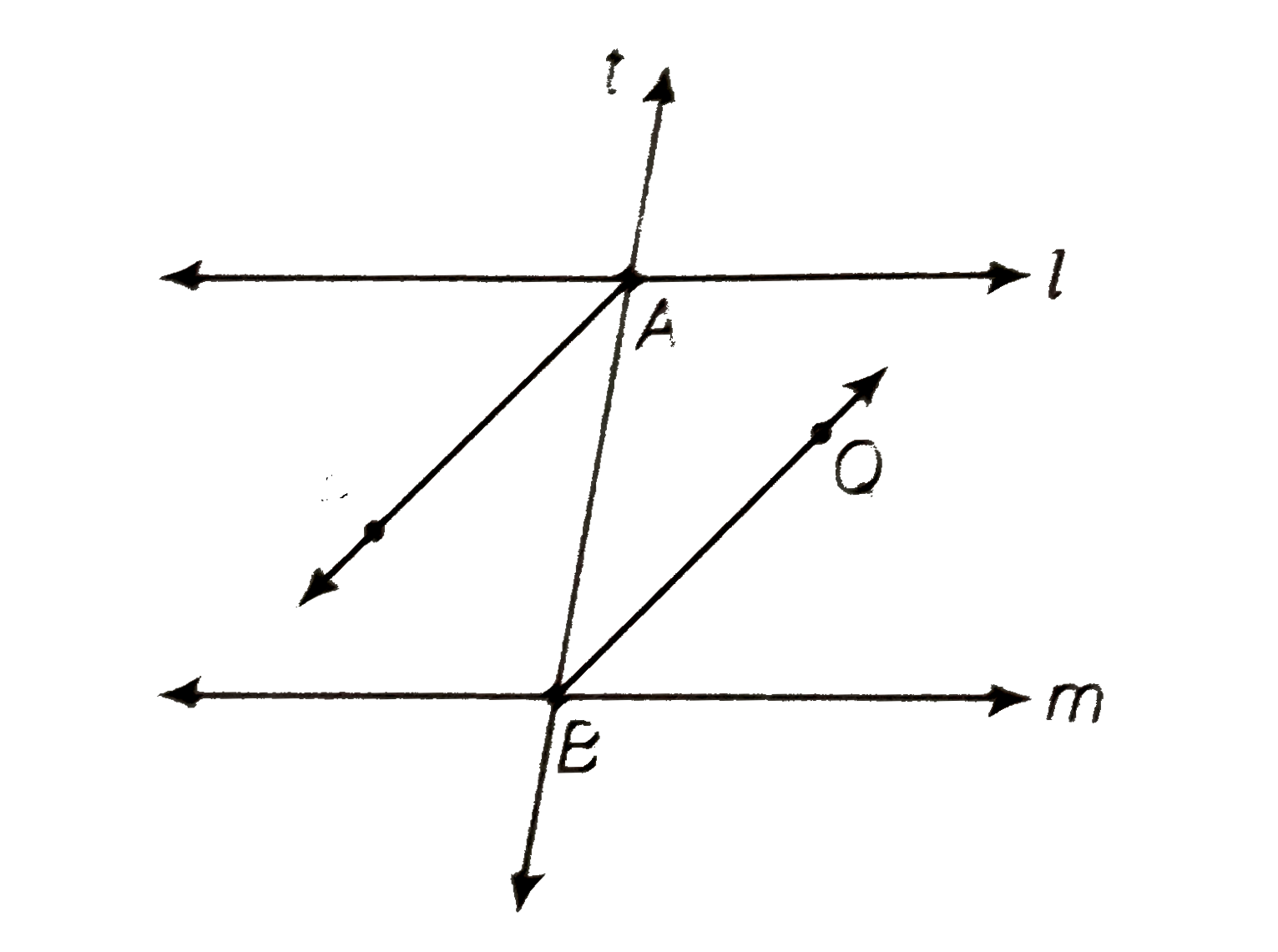
Given. In the figure AP ||BQ, AP and BQ are the bisectors of alternate interior angles
∠CABand∠ABF
To show l||m
proof Since, AP ||BQ and t is transversal, therefore ∠PAB=∠ABQ [alternate interior angles ]
⇒ 2∠PAB=2∠ABQ [multiplying both sides by 2]
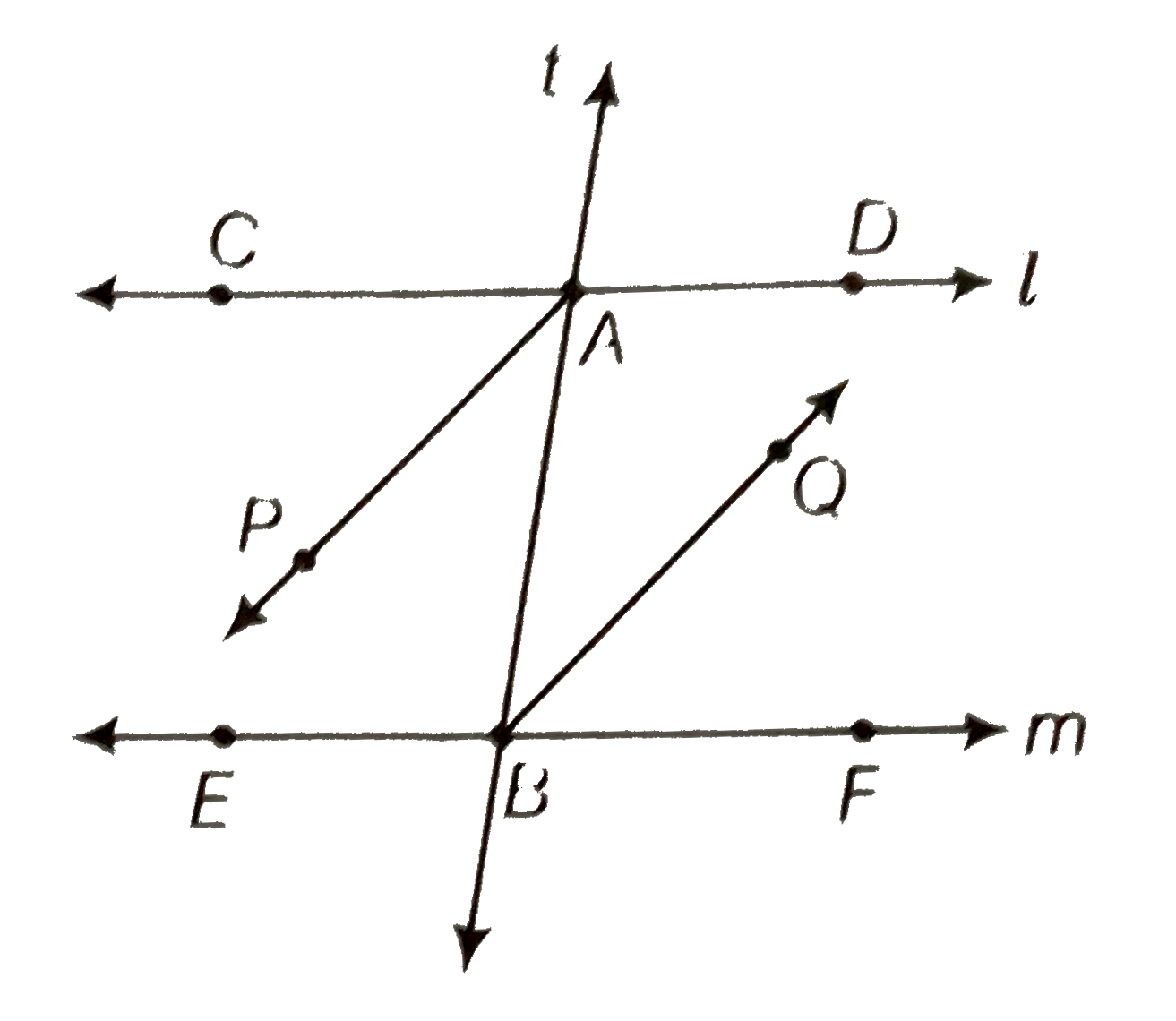
⇒ ∠CAB=∠ABF
So, alternate interior angles are equal.
We know that, if two alternate interior angles are equal, then lines are parallel.
Hence, l||m
Similar Questions
Knowledge Check
If two parallel lines are cut by a transversal, then the alternate interior angles are equal
ATRUEBFALSECCannot be determinedDNone of these
In the given figure, name the point in the interior of angle: (a) POQ (b) QOR
View SolutionIf two parallel lines are intersected by a transversal then prove that the bisectors of any pair of alternate interior angles are parallel.
View SolutionIn the given figure, AC>AB and AD is the bisector of ∠A. show that ∠ADC>∠ADB.
View Solution.In the given figure,if exterior angle is 105∘ and the interior opposite angles are equal.Find ∠A and ∠C
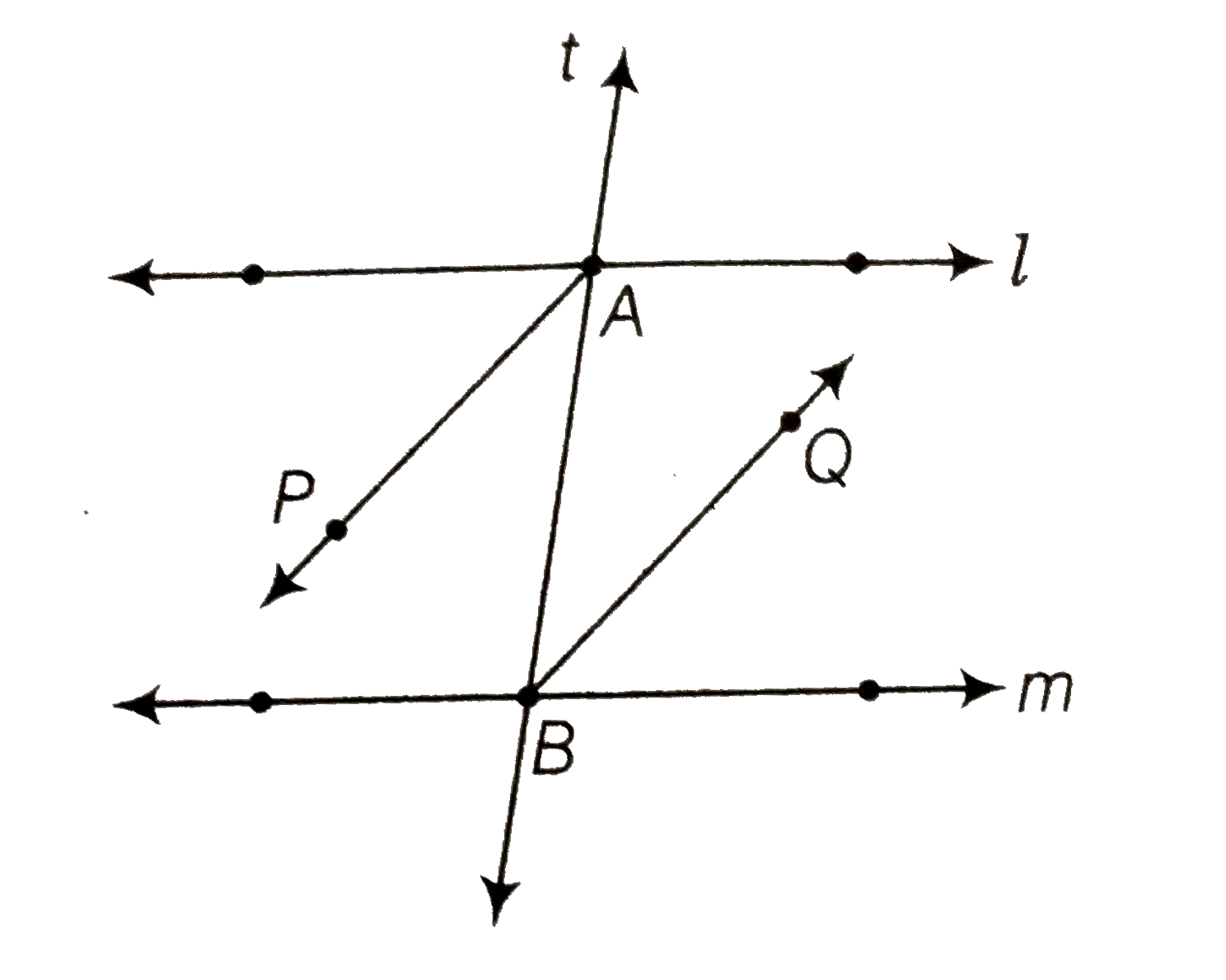
View SolutionAP and BQ are the bisectors of the two alternate interior angles formed by the intersection of a transversal t with parallel lines l and m (in the given figure). Show that AP||BQ.
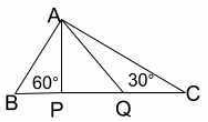
View SolutionIn the given figure, AP is perpendicular to BC, and AQ is the bisector ∠PAC. What will be the measure of ∠PAQ?
View SolutionIn the following figure, AB||CD, QM and RN are bisectors of alternate angles AQR and QRD respectively. Show that QM||RN.
View Solution
