If one of the zeroes of the cubic polynomial ax3+bx2+cx+d is zero, the product of the other two zeroes is
−ca
ca
0
−ba
The correct Answer is:B
To solve the problem, we need to analyze the cubic polynomial given and the implications of one of its zeroes being zero.
1. Identify the Polynomial:
We have a cubic polynomial given by P(x)=ax3+bx2+cx+d.
2. Understand the Zeroes:
A cubic polynomial can have three zeroes, which we can denote as α,β, and γ.
3. Given Condition:
We are told that one of the zeroes is zero. Let's assume α=0.
4. Using the Relationship of Zeroes:
According to Vieta's formulas, for a cubic polynomial ax3+bx2+cx+d, the relationships between the coefficients and the zeroes are:
- Sum of the zeroes: α+β+γ=−ba
- Sum of the product of the zeroes taken two at a time: αβ+βγ+γα=ca
- Product of the zeroes: αβγ=−da
5. Substituting the Known Zero:
Since we have α=0, we can substitute this into the second relationship:
0⋅β+β⋅γ+0⋅γ=ca
This simplifies to:
β⋅γ=ca
6. Conclusion:
Therefore, the product of the other two zeroes β and γ is given by:
β⋅γ=ca
Final Answer:
The product of the other two zeroes is ca.
We have a cubic polynomial given by P(x)=ax3+bx2+cx+d.
A cubic polynomial can have three zeroes, which we can denote as α,β, and γ.
We are told that one of the zeroes is zero. Let's assume α=0.
According to Vieta's formulas, for a cubic polynomial ax3+bx2+cx+d, the relationships between the coefficients and the zeroes are:
- Sum of the zeroes: α+β+γ=−ba
- Sum of the product of the zeroes taken two at a time: αβ+βγ+γα=ca
- Product of the zeroes: αβγ=−da
Since we have α=0, we can substitute this into the second relationship:
0⋅β+β⋅γ+0⋅γ=ca
This simplifies to:
β⋅γ=ca
Therefore, the product of the other two zeroes β and γ is given by:
β⋅γ=ca
The product of the other two zeroes is ca.
Similar Questions
Match the following :
If α,β,γ are zeroes of a cubic polynomial
ax3+bx2+cx+d(a≠0), then………
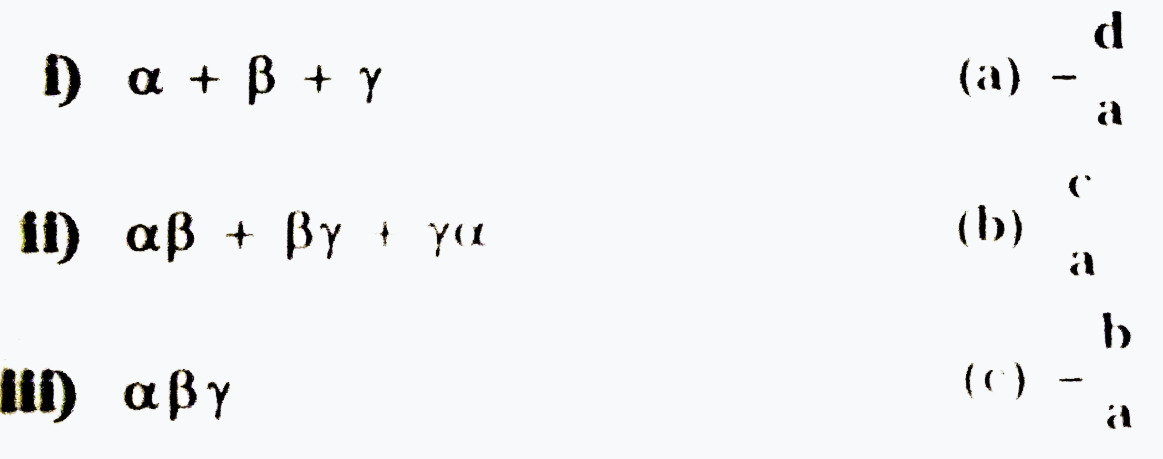
View SolutionMention the following with respect to the cubic polynomial ax3+bx2 + cx + d
(a) Sum of the zeroes
(b) Sum of the product of the zeroes, taken two at a time .
View SolutionAnswer the following by a number or a word or a sentence :
Given that one of the zeroes of the cubic polynomial ax3+bx2+cx+d is zero, what is the product of other two zeroes?
View Solutionत्रिघात बहुपद ax3+bx2+cx+d के दो शून्यक 0 दिए हैं। तीसरा शून्यक है
View SolutionTwo zeros of polynomial ax3+bx2+cx+dare zero then its third zero is
a/b
b/a
-b/a
d/c
View SolutionIf one of the zeroes of the cubic polynomial ax3+bx2+cx+d is zero, the product of the other two zeroes is :
View SolutionIf one of the zeroes of the cubic polynomial x^(3)+ax^(2)+bx+c is -1, then the product of the other two zeroes is
View SolutionTrighat polynomial ax^(3) + bx^(2) + cx + d No two zeros are given as 0, then the third zero is .............
View Solution
