In figure ABDC is a quadrant of a circle of a radius 28 cm and a semi circles BEC is drawn with BC as diameter find the area of shaded region:
To find the area of the shaded region in the given problem, we will follow these steps:
Step 1: Identify the components
We have a quadrant of a circle (ABDC) with a radius of 28 cm and a semicircle (BEC) with BC as the diameter. We need to find the area of the shaded region, which is the area of the quadrant minus the area of the semicircle.
Step 2: Calculate the area of the quadrant
The area of a quadrant of a circle is given by the formula:
Area of quadrant=14πr2
Substituting r=28 cm:
Area of quadrant=14×227×(28)2
Calculating (28)2=784:
Area of quadrant=14×227×784=22×78428=22×28=616 cm2
Step 3: Find the length of BC using Pythagoras theorem
In triangle ABC, we apply the Pythagorean theorem:
BC2=AB2+AC2
Given AB=28 cm and AC=28 cm:
BC2=282+282=784+784=1568
Thus,
BC=√1568=28√2 cm
Step 4: Calculate the radius of the semicircle
The radius of the semicircle BEC is half of BC:
Radius of semicircle=BC2=28√22=14√2 cm
Step 5: Calculate the area of the semicircle
The area of a semicircle is given by:
Area of semicircle=12πr2
Substituting r=14√2:
Area of semicircle=12×227×(14√2)2
Calculating (14√2)2=392:
Area of semicircle=12×227×392=22×39214=22×28=616 cm2
Step 6: Calculate the area of the shaded region
The area of the shaded region is:
Area of shaded region=Area of quadrant−Area of semicircle
Substituting the areas we calculated:
Area of shaded region=616−392=224 cm2
Final Answer
The area of the shaded region is 224 cm2.
---
We have a quadrant of a circle (ABDC) with a radius of 28 cm and a semicircle (BEC) with BC as the diameter. We need to find the area of the shaded region, which is the area of the quadrant minus the area of the semicircle.
The area of a quadrant of a circle is given by the formula:
Area of quadrant=14πr2
Substituting r=28 cm:
Area of quadrant=14×227×(28)2
Calculating (28)2=784:
Area of quadrant=14×227×784=22×78428=22×28=616 cm2
In triangle ABC, we apply the Pythagorean theorem:
BC2=AB2+AC2
Given AB=28 cm and AC=28 cm:
BC2=282+282=784+784=1568
Thus,
BC=√1568=28√2 cm
The radius of the semicircle BEC is half of BC:
Radius of semicircle=BC2=28√22=14√2 cm
The area of a semicircle is given by:
Area of semicircle=12πr2
Substituting r=14√2:
Area of semicircle=12×227×(14√2)2
Calculating (14√2)2=392:
Area of semicircle=12×227×392=22×39214=22×28=616 cm2
The area of the shaded region is:
Area of shaded region=Area of quadrant−Area of semicircle
Substituting the areas we calculated:
Area of shaded region=616−392=224 cm2
The area of the shaded region is 224 cm2.
Topper's Solved these Questions
- AREAS RELATED TO CIRCLESBOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - AREAS RELATED TO CIRCLESEXERCISE - LONG ANSWER TYPE QUESTIONS
10 Videos
- AREAS RELATED TO CIRCLESBOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - AREAS RELATED TO CIRCLESEXERCISE - PRACTICE-TEST ( AREAS RELATED TO CIRCLES ) SECTION-A
4 Videos
- AREAS RELATED TO CIRCLESBOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - AREAS RELATED TO CIRCLESEXERCISE - SHORT ANSWER TYPE I QUESTIONS
10 Videos
- ARITHMETIC PROGRESSION BOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - ARITHMETIC PROGRESSION EXERCISE - PRACTICE TEST (SECTION D)
1 Video
Similar Questions
Two circles touch externally. The sum of their areas is 130 πsq.cm. and the distance between their centres is 14cm. Find the radii of the circles.
View SolutionThe circumferences of two circles are in the ratio 2:3. What is the ratio between their areas?
The area of two circles are in the ratio 4:9. What is the ratio between their circumferences?
View SolutionFind the area of a quadrant of a circle whose circumference is 22 cm.
View SolutionIf the sum of three numbers in A.P., is 24 and their product is 440, find the numbers.
View SolutionBCP is a quadrant of a circle of radius 14cm. With AC as diameter,a semi-circle is drawn. Find the area of the shaded portion.
View SolutionIn the given figue, ABCD is a quadrant of a circle of radius 28 cm and a semicircle ABECA is drawn with AC as diameter. Find the area of the shaded region.
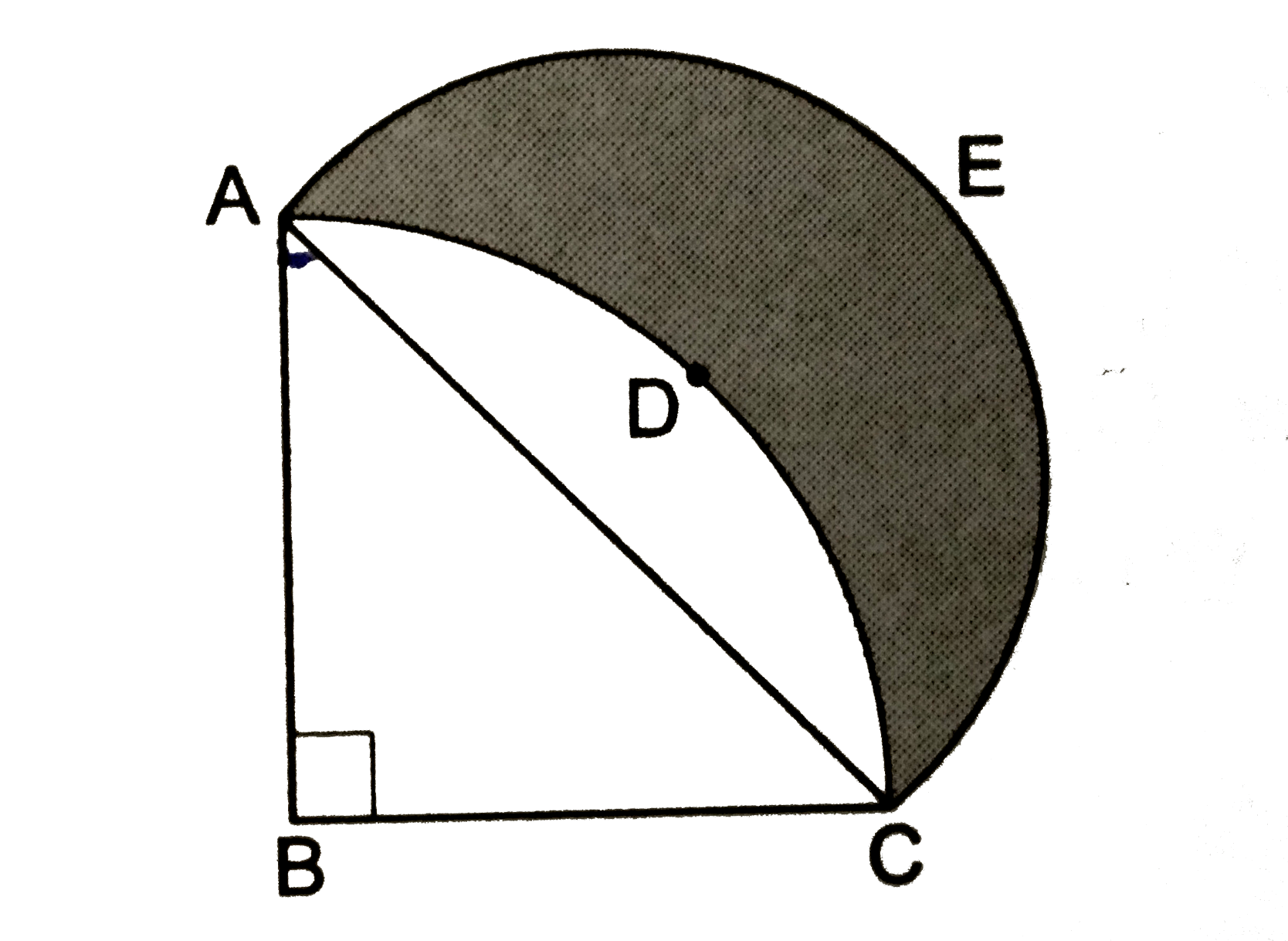
View Solutionआकृति में, ABC, त्रिज्या 14 सेमी वाले एक वृत का चतुर्थाश है तथा BC को व्यास मान कर एक अर्धवृत्त खींचा गया है छायांकित भाग का क्षेत्रफल ज्ञात कीजिए -
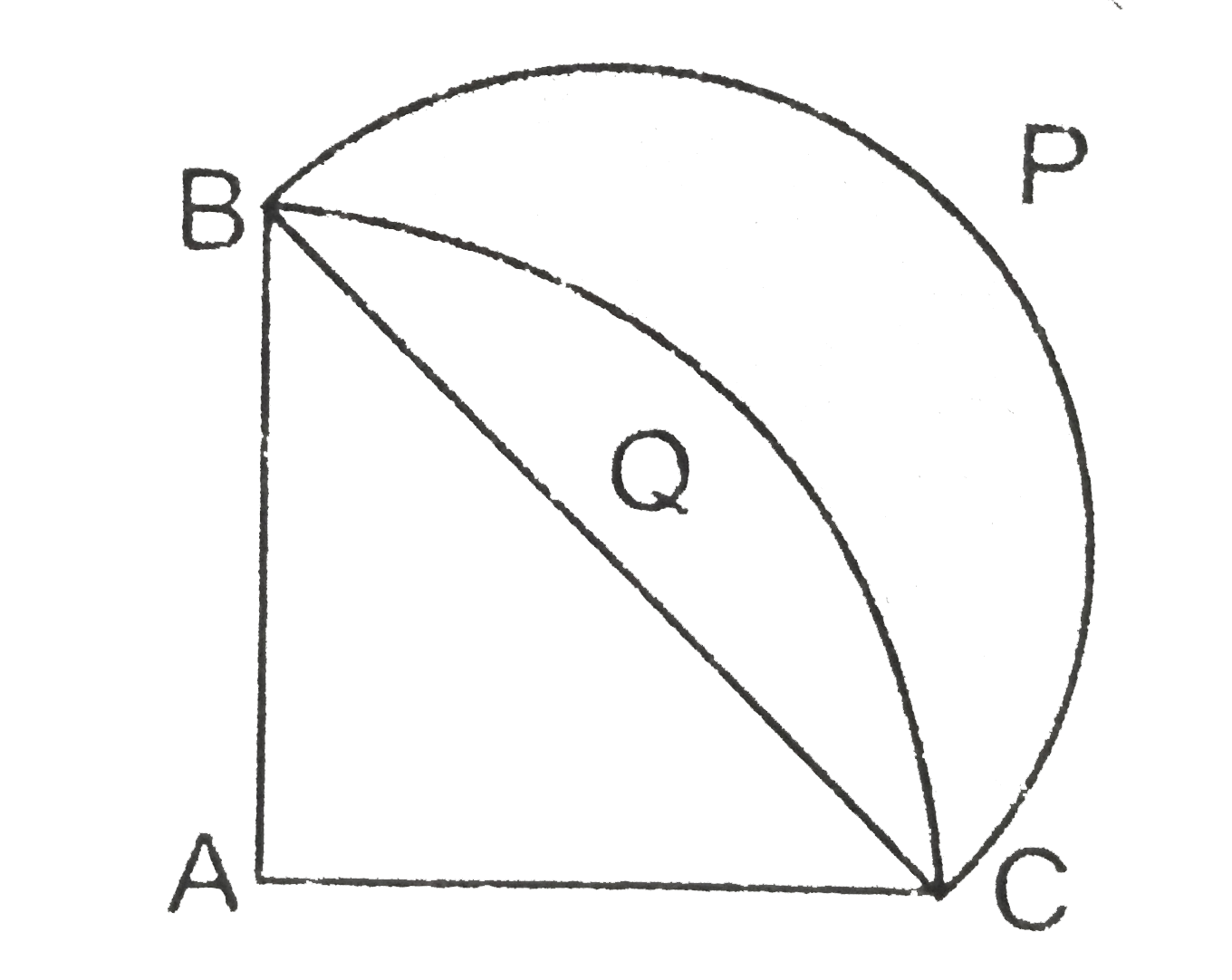
View Solution14 सेमी त्रिज्या वाले एक वृत्त का एक चतुर्थांश PQRA है अर्द्ध - वृत्त का व्यास PR द्वारा दर्शाया गया है तो छायांकित भाग का क्षेत्रफल ज्ञात कीजिए ।
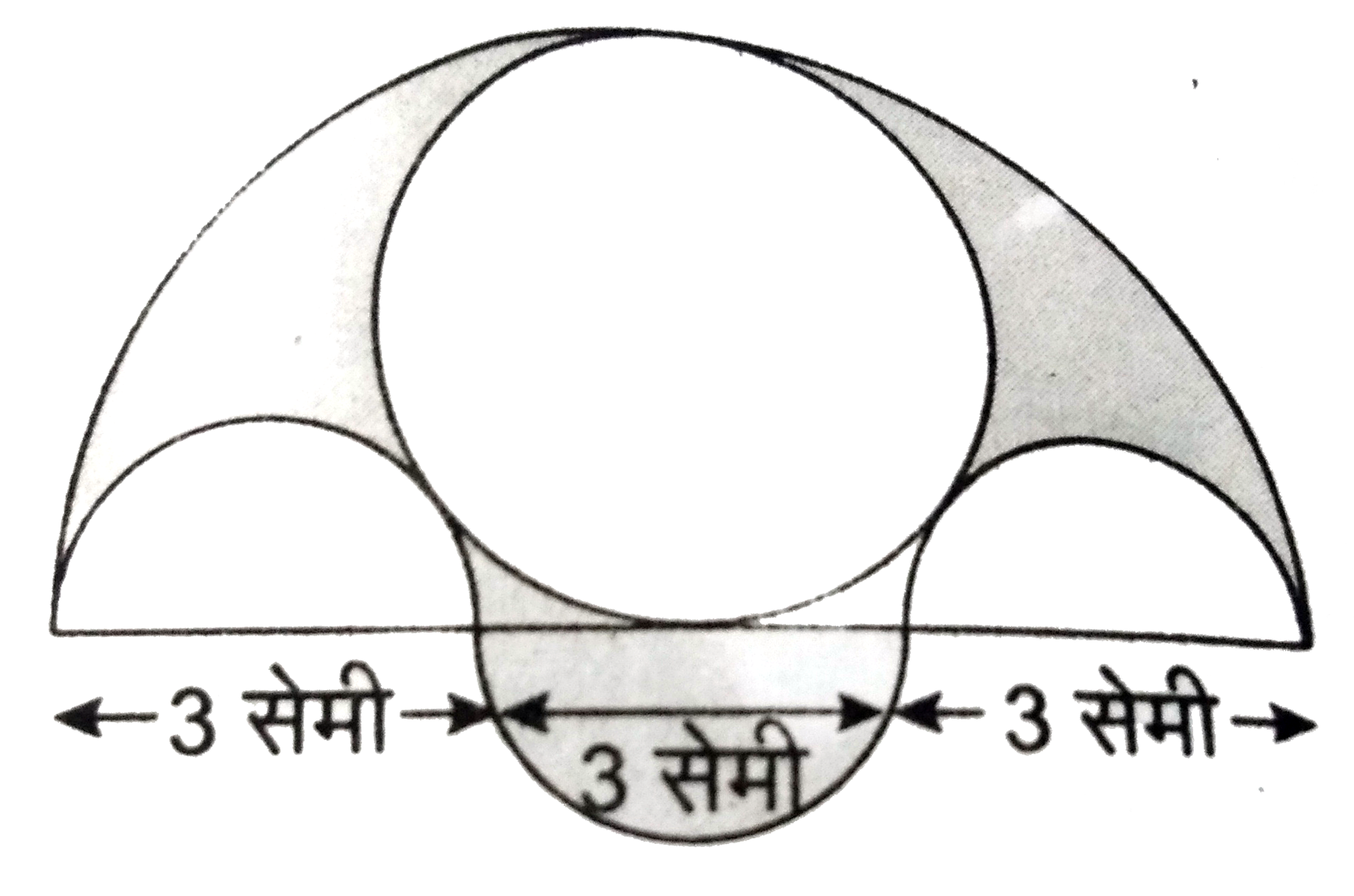
View Solutionसंलग्न आकृति में 3 सेमी व्यास के 3 अर्द्धवृत्त , 4.5 सेमी व्यास का के वृत्त और 4.5 सेमी त्रिज्या का एक वृत्त खींचे गये है । छायांकित भाग का क्षेत्रफल ज्ञात कीजिए ।
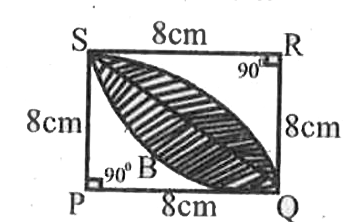
View SolutionFind the area of the shaded region. In the given figure common between the two quadrants of circles of radius 8cm each.
OR
In fig. ABC is a quadrant of a circle of radius 14cm and a semicircle is drawn with BC as diameter. Find the area of the shaded region.
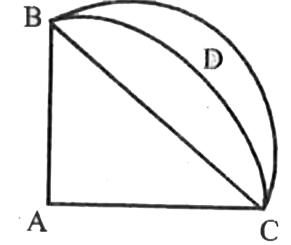
View SolutionIn Fig. 12.33, ABC is a quadrant of a circle of radius 14 cm and a semicircle is drawn with BC as diameter. Find the area of the shaded region.
View SolutionIn the fig.ABC is a quadrant of a circle of radius 14cm and a semicircle is drawn with BC as a diameter. Find the area of the shaded region.
View SolutionIn Fig. 12.33, ABC is a quadrant of a circle of radius 14 cm and a semicircle is drawn with BC as diameter. Find the area of the shaded region.
View SolutionCircle inside a Circle : PQRS is a diameter of a circle of radius 6 cm. The length PQ, QR and RS are equal. Semi circles are drawn on PQ and QS as diameters, as shown in Figure. Find the perimeter and area of shaded Region.
View SolutionABCP is a quadrant of a circle of radius 14 cm. With AC as diameter, a semi-circle is drawn. Find the area of the shaded portion.
View Solution
