A cylindrical conductor of radius R carrying current i along the axis such that the magnetic field inside the conductor varies as B=B0r2(0<r≤R), then which of the following in incorrect?
Current density at distance 'r' from central axis of the conductor is J(r)=2B0rμ0
Current density at distance 'r' from central axis of the conductor is J(r)=3B0rμ0
Half of the total current would be confined within the radius of R(2)13 of the conductor
For r>R magnetic field would vary as B(r)=B0R3r
The correct Answer is:A
To solve the problem, we need to analyze the given information about the cylindrical conductor and the magnetic field inside it. The magnetic field B is given as B=B0r2 for 0<r≤R.
1. Understanding the Magnetic Field:
- The magnetic field inside the conductor varies with the radius r as B=B0r2. This indicates that the magnetic field strength increases with the square of the distance from the axis of the cylinder.
2. Finding Current Density:
- The magnetic field B is related to the current density J through Ampere's Law. Since B depends on r2, the current density J must also vary with r.
- We can express the current density as J(r)=krn, where k is a constant and n is a power that we need to determine.
3. Using Ampere's Law:
- According to Ampere's Law, for a cylindrical conductor, the integral form is given by:
∮B⋅dl=μ0Ienc
- For a circular path of radius r, the left-hand side becomes B⋅2πr.
4. Calculating Enclosed Current:
- The enclosed current Ienc for a radius r is given by:
Ienc=∫r0J(r′)⋅dA=∫r0J(r′)⋅2πr′dr′
- Substituting J(r′)=kr′n:
Ienc=2πk∫r0r′n+1dr′=2πk(rn+2n+2)r0=2πkrn+2n+2
5. Equating Both Sides:
- From Ampere's Law:
B⋅2πr=μ0Ienc
- Substituting B=B0r2 and Ienc:
(B0r2)⋅2πr=μ0(2πkrn+2n+2)
- Simplifying gives:
2πB0r3=2πμ0krn+2n+2
- Canceling 2π and rearranging:
B0r3=μ0krn+2n+2
6. Comparing Powers:
- For the powers of r to match, we have:
3=n+2⟹n=1
- Substituting n=1 into the equation gives:
B0=μ0k3
7. Finding Current Density:
- Thus, the current density becomes:
J(r)=kr=3B0r/μ0
8. Analyzing the Options:
- Now we need to determine which of the provided options is incorrect based on our findings about J and the behavior of B.
Conclusion:
After analyzing the behavior of the magnetic field and the current density, we can conclude that:
- Option A: Correct
- Option B: Correct
- Option C: Correct
- Option D: Incorrect (as it does not follow the derived relationship for B when r>R)
- The magnetic field inside the conductor varies with the radius r as B=B0r2. This indicates that the magnetic field strength increases with the square of the distance from the axis of the cylinder.
- The magnetic field B is related to the current density J through Ampere's Law. Since B depends on r2, the current density J must also vary with r.
- We can express the current density as J(r)=krn, where k is a constant and n is a power that we need to determine.
- According to Ampere's Law, for a cylindrical conductor, the integral form is given by:
∮B⋅dl=μ0Ienc
- For a circular path of radius r, the left-hand side becomes B⋅2πr.
- The enclosed current Ienc for a radius r is given by:
Ienc=∫r0J(r′)⋅dA=∫r0J(r′)⋅2πr′dr′
- Substituting J(r′)=kr′n:
Ienc=2πk∫r0r′n+1dr′=2πk(rn+2n+2)r0=2πkrn+2n+2
- From Ampere's Law:
B⋅2πr=μ0Ienc
- Substituting B=B0r2 and Ienc:
(B0r2)⋅2πr=μ0(2πkrn+2n+2)
- Simplifying gives:
2πB0r3=2πμ0krn+2n+2
- Canceling 2π and rearranging:
B0r3=μ0krn+2n+2
- For the powers of r to match, we have:
3=n+2⟹n=1
- Substituting n=1 into the equation gives:
B0=μ0k3
- Thus, the current density becomes:
J(r)=kr=3B0r/μ0
- Now we need to determine which of the provided options is incorrect based on our findings about J and the behavior of B.
After analyzing the behavior of the magnetic field and the current density, we can conclude that:
- Option B: Correct
- Option C: Correct
- Option D: Incorrect (as it does not follow the derived relationship for B when r>R)
Similar Questions
The magnetic field on the axis of a circular current carrying conductor of radius r at a distance r from centre is B_(a) and the magnetic field at its centre is B_(c ) . The value of B_(a) : B_(c ) is
View SolutionFind the magnitude of the magnetic induction B of a magnetic field generated by a system of thin conductors along which a current I is flowing at a point A (O, R, O), that is the centre of a circular conductor of radius R. The ring is in yz plane.
View SolutionA long cylindrical conductor of radius R carries a current i as shown in the figure. The current density J varies across the cross-section as J = kr^(2) , where, k is a constant. Find an expression for the magnetic field B at a distance r (lt R) from the axis
View SolutionFind the magnitude of the magnetic induction B of a magnetic field generated by a system of thin conductors along which a current I is flowing at a point A (O, R, O), that is the centre of a circular conductor of radius R. The ring is in yz plane.
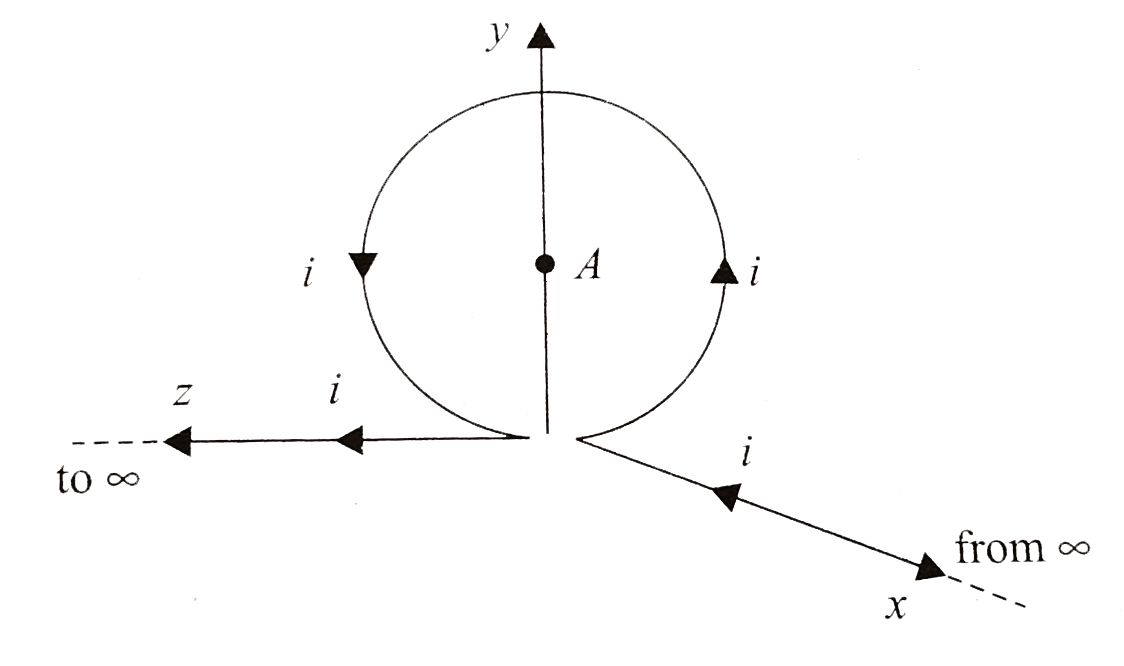
View SolutionA cylindrical conductor of radius R is carrying a constant current. The plot of the magnitude of the magnetic field, B with the distance, d from the centre of the conductor, is correctly represented by the figure
View SolutionA cylindrical conductor of radius R carrying current i along the axis such that the magnetic field inside the conductor varies as B=B0r2(0<r≤R), then which of the following in incorrect?
View SolutionA cylindrical conductor of radius R is carrying a constant current. The plot of the magnitude of the magnetic field B with the distance d from the centre of the conductor, is correctly represented by the figure :
View SolutionA cylindrical conductor of radius R which carries a current i along the axis such that the magnetic field inside the conductor B=B_(0)r^(2)(0ltrleR) then which of the following is wrong?
View Solution
