Two ships are sailling in the sea on the two sides of a lighthouse. If the distance between the ships is 10(√3+1) meters and their angle of elevations of the top of the lighthouse are 60∘and45∘, then the height of the lighthouse is (The two ships and the foot of lighthouse are in a straight line)
20 meters
20√3 meters
10√3 meters
5√3 meters
The correct Answer is:C
To solve the problem step by step, we will denote the height of the lighthouse as h (or X as mentioned in the transcript). We will also denote the distances from the base of the lighthouse to the ships as follows:
- Let S1 be the ship on one side of the lighthouse, and let the distance from the base of the lighthouse to S1 be y.
- Let S2 be the ship on the other side of the lighthouse, and let the distance from the base of the lighthouse to S2 be z.
Given:
- The distance between the two ships S1 and S2 is y+z=10(√3+1).
- The angle of elevation from S1 (where the angle is 60∘) and from S2 (where the angle is 45∘).
Step 1: Set up the equations using trigonometric ratios
1. For ship S2 (angle of elevation 45∘):
tan(45∘)=hz
Since tan(45∘)=1:
h=z(Equation 1)
2. For ship S1 (angle of elevation 60∘):
tan(60∘)=hy
Since tan(60∘)=√3:
√3=hy⟹h=y√3(Equation 2)
Step 2: Substitute and solve for h
From Equation 1, we have:
z=h
From Equation 2, we have:
y=h√3
Step 3: Substitute y and z into the distance equation
Substituting y and z into the distance equation:
y+z=10(√3+1)
Substituting the values of y and z:
h√3+h=10(√3+1)
Step 4: Combine terms
Combine the terms on the left:
h(1√3+1)=10(√3+1)
Step 5: Solve for h
To simplify:
h(1+√3√3)=10(√3+1)
Now, multiply both sides by √3:
h(1+√3)=10√3(√3+1)
Calculating the right side:
10√3(√3+1)=10(3+√3)=30+10√3
Now, divide both sides by 1+√3:
h=30+10√31+√3
Step 6: Rationalize the denominator
Multiply the numerator and denominator by the conjugate of the denominator:
h=(30+10√3)(1−√3)(1+√3)(1−√3)
Calculating the denominator:
(1+√3)(1−√3)=1−3=−2
Calculating the numerator:
(30+10√3)(1−√3)=30−30√3+10√3−30=−20√3
Thus:
h=−20√3−2=10√3
Final Answer:
The height of the lighthouse is 10√3 meters.
- Let S2 be the ship on the other side of the lighthouse, and let the distance from the base of the lighthouse to S2 be z.
- The distance between the two ships S1 and S2 is y+z=10(√3+1).
- The angle of elevation from S1 (where the angle is 60∘) and from S2 (where the angle is 45∘).
tan(45∘)=hz
Since tan(45∘)=1:
h=z(Equation 1)
tan(60∘)=hy
Since tan(60∘)=√3:
√3=hy⟹h=y√3(Equation 2)
z=h
From Equation 2, we have:
y=h√3
y+z=10(√3+1)
Substituting the values of y and z:
h√3+h=10(√3+1)
h(1√3+1)=10(√3+1)
h(1+√3√3)=10(√3+1)
Now, multiply both sides by √3:
h(1+√3)=10√3(√3+1)
Calculating the right side:
10√3(√3+1)=10(3+√3)=30+10√3
Now, divide both sides by 1+√3:
h=30+10√31+√3
h=(30+10√3)(1−√3)(1+√3)(1−√3)
Calculating the denominator:
(1+√3)(1−√3)=1−3=−2
Calculating the numerator:
(30+10√3)(1−√3)=30−30√3+10√3−30=−20√3
Thus:
h=−20√3−2=10√3
The height of the lighthouse is 10√3 meters.
Topper's Solved these Questions
Similar Questions
Find the coordinates the those point on the line 3x+2y=5 which are equisdistant from the lines 4x+3y−7=0and2y−5=0
View SolutionThe greatest term in the expansion of (3+2x)51, where x=15, is
View SolutionThe angle of depression of a ship as observed from the top of a lighthouse is 45∘ . If the height of the lighthouse is 200 m , then what is the distance of the ship from the foot of the lighthouse ?
View Solutionएक प्रकाश-स्तम्भ के शीर्ष से, विपरीत दिशाओं में स्थित दो जहाजों के अवनमन कोण 30∘ और 45∘ हैं। यदि प्रकाश-स्तम्भ की ऊँचाई 90 मीटर है तथा दोनों जहाजों को मिलाने वाली रेखा प्रकाश-स्तम्भ के पाद से होकर जाती है, तो दोनों जहाजों के बीच की दूरी ज्ञात कीजिए।
View SolutionAs observed from the top of a 75m high lighthouse from the sea-level, the angles of depression of two ships are 30∘ and 45∘ . If one ship is exactly behind the other on the same side of the lighthouse, find the distance between the two ships.
View SolutionTwo ships are sailing in the sea on the two side of lighthouse of height 10 m . The angle of elevation to the top of lighthouse observed from the ships are 30^@ and 45^@ then distance between two ship is [use sqrt(3)=1.7 ]
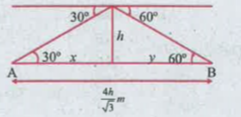
View Solutionஒரு கலங்கரை விளக்கத்தின் உச்சியிலிருந்து எதிரெதிர்பக்கங்களில் உள்ள இரண்டு கப்பல்கள் 30∘ மற்றும் 60∘இறக்கக் கோணத்தில் பார்க்கப்படுகின்றன.கலங்கரை விளக்கத்தின் உயரம் h மீ. இரு கப்பல்கள் மற்றும் கலங்கரை விளக்கத்தின் அடிப்பகுதி ஆகியவை ஒரே நேர்கோட்டில் அமைகின்றன எனில், இரண்டு கப்பல்களுக்கு இடைப்பட்ட தொலைவு 4h√3 மீ என நிரூபிக்க.
View Solution60 मीटर ऊँचे प्रकाश स्तम्भ की चोटी से एक जहाज का अवनमन कोण 60 है तो प्रकाश स्तम्भ पद से जहाज की दूरी ज्ञात कीजिए।
View SolutionThe angles of depression of two ships from the top of a lighthouse are 45∘and30∘. If the ships are 120 m apart, then find the height of the lighthouse.
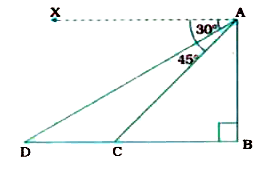
View SolutionAs observed from the top of a 75m high lighthouse from the sea-level, the angles of depression of two ships are 30∘and45∘. If one ship is exactly behind the other on the same side of the lighthouse, find the distance between the two ships
View SolutionThe angle of depression of a ship as observed from the top of a lighthouse is 45∘ . If the height of the lighthouse is 200 m , then what is the distance of the ship from the foot of the lighthouse ?
View Solutionकिसी प्रकाशघर के विपरीत किनारों पर से देखने पर स्थित दो जहाजों के अवनमन कोण 30∘ तथा 45∘ देखे गए हैं यदि प्रकाशघर की ऊँचाई 300 मी हो और यदि उनको मिलाने वाली रेखा प्रकाशघर के आधार से गुजरती हो, तो जहाजों के बीच की दूरी है (√3=1.7321)
View Solutionएक लाइट हाउस से इसके विपरीत दिशाओं में स्थित दो जहाजों के अवनमन कोण क्रमशः 30∘ और 45∘ है यदि लाइट हाउस की ऊँचाई 100 m हो तो दोनों जहाजों के बीच की दूरी ज्ञात कीजिए यदि दोनों जहाजों को मिलाने वाली रेखा लाइट हाउस के पाद से जाती है।
View SolutionTwo ships are sailing in the sea on the two sides of a lighthouse. The angle of elevation of the top of the lighthouse is observed from the ships are 30° and 45° respectively. If the lighthouse is 100 m high, the distance between the two ships is:
View SolutionTwo ships are sailling in the sea on the two sides of a lighthouse. If the distance between the ships is 10(√3+1) meters and their angle of elevations of the top of the lighthouse are 60∘and45∘, then the height of the lighthouse is (The two ships and the foot of lighthouse are in a straight line)
View Solution
