A clear sheet of polaroid is placed on the top of similar sheet so that their axes make an angle sin−1(35) with each other. The ratio of intensity of the emergent light to that of unpolarised incident light is
16:25
9:25
4:5
8:25
The correct Answer is:D
To solve the problem, we need to find the ratio of the intensity of the emergent light to that of the unpolarized incident light when two polaroid sheets are placed at an angle of sin−1(3/5) with respect to each other.
1. Understanding the Incident Light:
The incident light is unpolarized. The intensity of the unpolarized light is denoted as I0.
2. First Polarizer:
When unpolarized light passes through the first polarizer, the intensity of the transmitted light is reduced to half of the incident intensity. Therefore, the intensity after the first polarizer, I1, is given by:
I1=I02
3. Angle Between the Polarizers:
The angle between the transmission axes of the two polarizers is given as θ=sin−1(3/5).
4. Calculating cosθ:
To use Malus's law, we need to find cosθ. We can calculate it using the identity:
cos2θ=1−sin2θ
Given sinθ=35:
sin2θ=(35)2=925
Therefore,
cos2θ=1−925=1625
Thus,
cosθ=√1625=45
5. Second Polarizer:
The intensity of light after passing through the second polarizer can be calculated using Malus's law:
Iemergent=I1⋅cos2θ
Substituting the values we have:
Iemergent=(I02)⋅(1625)
Simplifying this gives:
Iemergent=16I050=8I025
6. Finding the Ratio:
The ratio of the intensity of the emergent light to that of the unpolarized incident light is:
IemergentI0=8I025I0=825
Final Answer:
The ratio of the intensity of the emergent light to that of the unpolarized incident light is:
825
The incident light is unpolarized. The intensity of the unpolarized light is denoted as I0.
When unpolarized light passes through the first polarizer, the intensity of the transmitted light is reduced to half of the incident intensity. Therefore, the intensity after the first polarizer, I1, is given by:
I1=I02
The angle between the transmission axes of the two polarizers is given as θ=sin−1(3/5).
To use Malus's law, we need to find cosθ. We can calculate it using the identity:
cos2θ=1−sin2θ
Given sinθ=35:
sin2θ=(35)2=925
Therefore,
cos2θ=1−925=1625
Thus,
cosθ=√1625=45
The intensity of light after passing through the second polarizer can be calculated using Malus's law:
Iemergent=I1⋅cos2θ
Substituting the values we have:
Iemergent=(I02)⋅(1625)
Simplifying this gives:
Iemergent=16I050=8I025
The ratio of the intensity of the emergent light to that of the unpolarized incident light is:
IemergentI0=8I025I0=825
The ratio of the intensity of the emergent light to that of the unpolarized incident light is:
825
Topper's Solved these Questions
Similar Questions
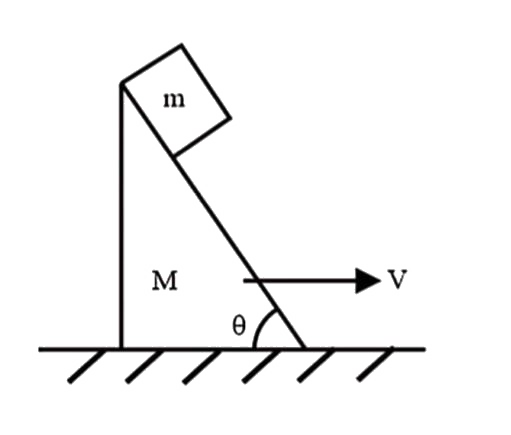
A block of mass m is stationary with respect to the wedge of mass M moving with uniform speed v on horizontal surface. Work done by friction force on the block in t seconds is
View SolutionAssuming the mass of the earth as 6.64×1024kg Kg and the average mass of the atoms that make up the earth as 40 u ( atomic mass. Unit ) , the number of atoms in the earth is approximately
View SolutionUnpolarised light falls on two polarizing sheets placed one on top of the other. What must be the angle between the characteristic directions of the sheets if the intensity of the final transmitted light is one-third the maximum intensity of the first transmitted beam?
View SolutionAt what angle should the axes of two polaroids be placed so as to reduce the intensity of incident unpolarized light to 1/3.
View SolutionTwo polaroid sheets are placed one over the other with their axes inclied to each other at an angle theta . If only 12.5% of the intensity of the light incident on the first sheet emerges out from the second sheet, the value of theta is
View SolutionA transparent thin plate of a polaroid is placed on another similar plate such that the angle between their axes is 30^(@) . The intensities of the emergent and the upolarized incident light will be in the ratio of
View SolutionA clear sheet of polaroid is placed on top of a similar sheet so that axews make an angle of sin−1(45) with each other. The ratio of intensity of the emergent light to that of polarised light is
View SolutionThe optic axis of two polaroids are inclined at an angle of 45∘ with each other. Unpolarised light of intensity I0 being incident on the first polaroid emerges from the second polaroid. Find the intensity of the emergent light.
View SolutionTo reduce the intensity of incident unpolarised light to 1//4 , find the angle at which the axes of two polaroids should be placed.
View SolutionA transparent thin plate of a polaroid is placed on another similar plate such that the angle between their axes is 30∘. The intensities of the emergent and the upolarized incident light will be in the ratio of
View SolutionUnpolarised light of intensity l0 passes through five successive polaroid sheets,each of whose transmission axes makes an angle 45^. With the previous one.The intensity of the finally transmitted light is
View SolutionUnpolarised light falls on two polarizing sheets placed one on top of the other. What must be the angle between the characteristic directions of the sheets if the intensity of the final transmitted light is one-third the maximum intensity of the first transmitted beam?
View SolutionA clear sheet of polaroid is placed on top of a similar sheet so that axews make an angle of sin−1(45) with each other. The ratio of intensity of the emergent light to that of polarised light is
View SolutionUnpolarised light falls on two polarising sheets placed one on top of the other. What must be the angle between the characteristic directions of the sheets if the intensity of the final transmitted light is one-third the maximum intensity of the first transmitted beam?
View SolutionTwo polaroid sheets are placed one over the other with their axes inclined to each other at 30∘. The ratio of the intensity of the unpolarised incident light and the polarised emergent light is :
View Solution
