A cylindrical wire of radius R has current density varying with distance r form its axis as J(x)=J0(1−r2R2) . The total current through the wire is
πJ0R22
2πJ0R23
4πJ0R23
none of these
The correct Answer is:A
To find the total current through a cylindrical wire with a varying current density, we can follow these steps:
Step 1: Understand the Given Current Density
The current density J(r) is given by:
J(r)=J0(1−r2R2)
where J0 is a constant, r is the distance from the axis of the cylinder, and R is the radius of the cylinder.
Step 2: Define a Differential Current Element
To find the total current, we will consider a thin cylindrical shell of radius r and thickness dr. The differential area dA of this shell is given by the circumference times the thickness:
dA=2πrdr
Step 3: Express the Differential Current
The differential current dI flowing through this shell can be expressed as:
dI=J(r)⋅dA=J0(1−r2R2)⋅(2πrdr)
Step 4: Integrate to Find Total Current
To find the total current I, we integrate dI from r=0 to r=R:
I=∫R0dI=∫R0J0(1−r2R2)(2πrdr)
Step 5: Simplify the Integral
We can factor out the constants:
I=2πJ0∫R0(1−r2R2)rdr
Now, we can split the integral:
I=2πJ0(∫R0rdr−1R2∫R0r3dr)
Step 6: Calculate the Integrals
1. The first integral:
∫R0rdr=(r22)R0=R22
2. The second integral:
∫R0r3dr=(r44)R0=R44
Step 7: Substitute Back into the Equation
Substituting these results back into the equation for I:
I=2πJ0(R22−1R2⋅R44)
I=2πJ0(R22−R24)
I=2πJ0(2R24−R24)=2πJ0⋅R24
Step 8: Final Result
Thus, the total current I through the wire is:
I=πJ0R22
---
The current density J(r) is given by:
J(r)=J0(1−r2R2)
where J0 is a constant, r is the distance from the axis of the cylinder, and R is the radius of the cylinder.
To find the total current, we will consider a thin cylindrical shell of radius r and thickness dr. The differential area dA of this shell is given by the circumference times the thickness:
dA=2πrdr
The differential current dI flowing through this shell can be expressed as:
dI=J(r)⋅dA=J0(1−r2R2)⋅(2πrdr)
To find the total current I, we integrate dI from r=0 to r=R:
I=∫R0dI=∫R0J0(1−r2R2)(2πrdr)
We can factor out the constants:
I=2πJ0∫R0(1−r2R2)rdr
Now, we can split the integral:
I=2πJ0(∫R0rdr−1R2∫R0r3dr)
1. The first integral:
∫R0rdr=(r22)R0=R22
2. The second integral:
∫R0r3dr=(r44)R0=R44
Substituting these results back into the equation for I:
I=2πJ0(R22−1R2⋅R44)
I=2πJ0(R22−R24)
I=2πJ0(2R24−R24)=2πJ0⋅R24
Thus, the total current I through the wire is:
I=πJ0R22
Similar Questions
In a long cylindrical wire of radius R, magnetic induction varies with the distance from axis as B=crα. Find the function of current density in wire with the distance from axis of wire.
View SolutionA current is flowing through a cylinderical conductor of radius R, such that current density at any cross-section is given by J=J0(1−rR), where r is radial distance from axis of the cylinder .Calculate the total current through the cross-section of the conductor.
View Solution
Knowledge Check
An infinite cylindrical wire of radius R and having current density varying with its radius r as, J=J0[1−(r/R)]. Then answer the following questions.
Graph between the magnetic field and radius isA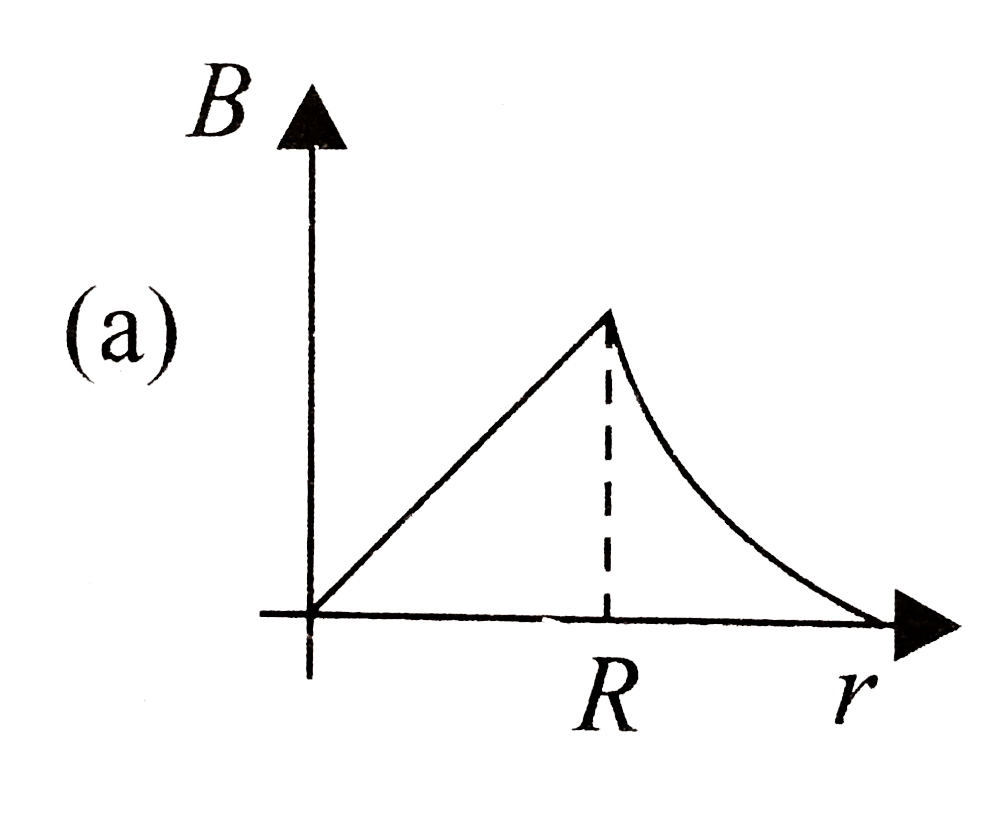 B
B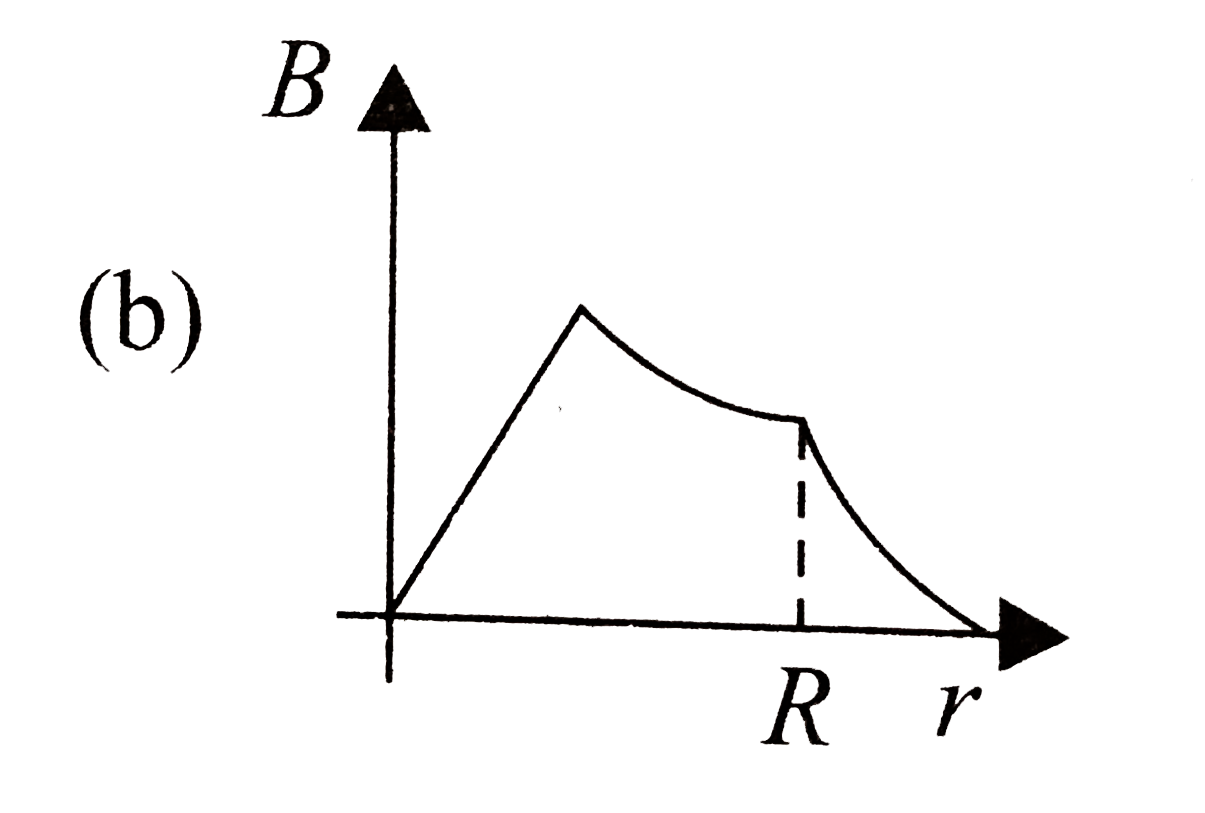 C
C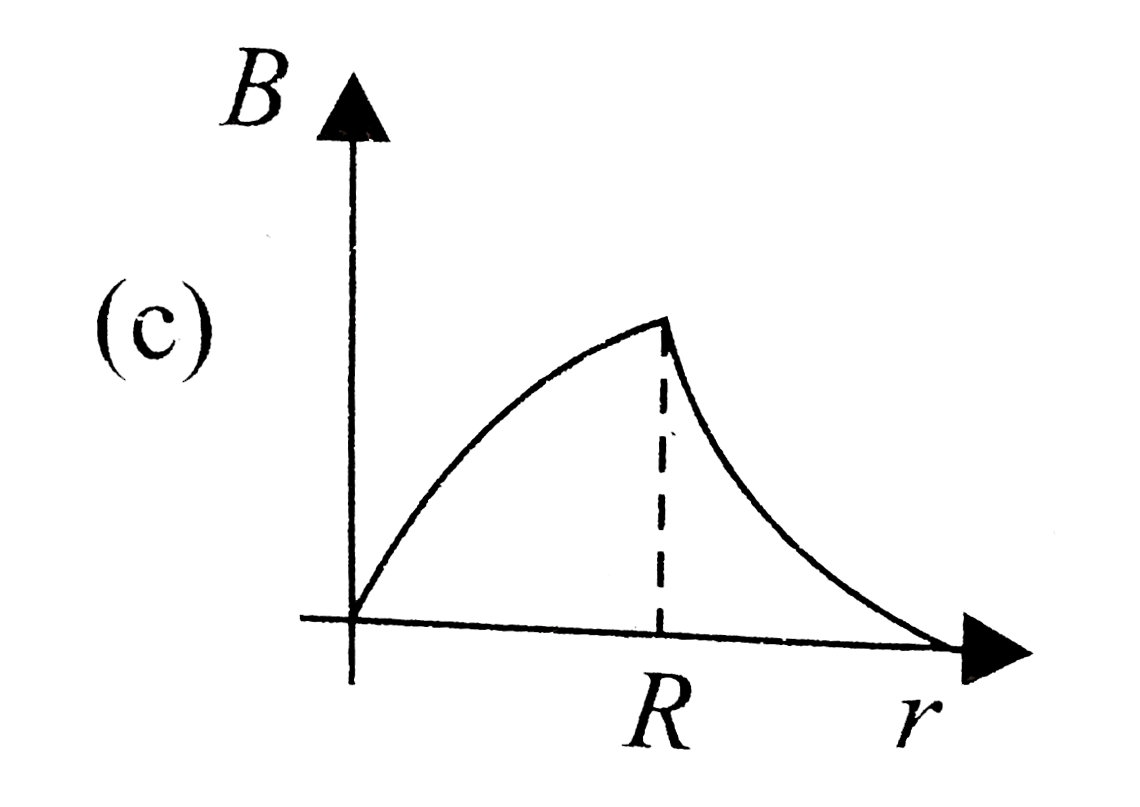 D
D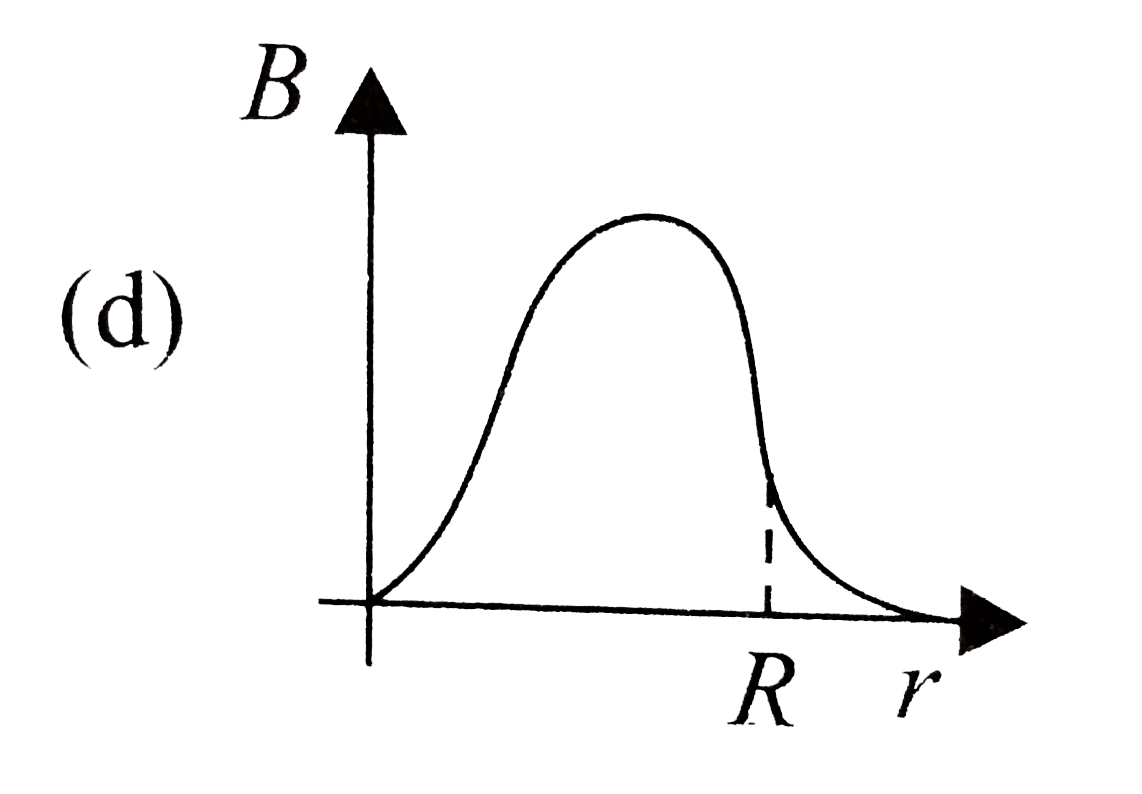
An infinite cylindrical wire of radius R and having current density varying with its radius r as, J=J0[1−(r/R)]. Then answer the following questions.
Position where magnetic field strength is maximum.ARB3R/4Cr/2DR/4An infinite cylindrical wire of radius R and having current density varying with its radius r as, J=J0[1−(r/R)]. Then answer the following questions.
Magnitude of maximum magnetic field isAJ0R6μ0B316J0Rμ0C516J0Rμ0D56J0Rμ0
(a) The current density in a cylindrical wire of radius R=2.0mm is uniform across a cross section of the wire and is J=2.0×105A/m2. What is the current through the outer portion of the wire between radial distances R/2 and R?
(b) Suppose, instead, the current density through a cross section varies with radial distance r as J=ar2, in which a=3.0×1011A/m4 and r is in meters. What now is the current through the same outer portion of the wire?
View SolutionThe mass density of a planet of radius R varie with the distance r form its centre as ρ(r)=p0(1−r2R2). Then the graviational field is maximum at :
View SolutionThe current density across a cylindrical conductor of radius R varies in magnitude according to the equation J=J0(1−rR) where r is the distance from the central axis. Thus, the current density is a maximum J0 at that axis (r = 0) and decreases linearly to zero at the surface (r = R). Calculate the current in terms of J0 and the conductor 's cross - sectional area A=πR2.
View SolutionThe current density is a solid cylindrical wire a radius R, as a function of radial distance r is given by J(r)=J0(1−rR) . The total current in the radial regon r = 0 to r=R4 will be :
View SolutionFor a long wire of charge density γ,, field at a distance r from the wire is
View Solution
