Find the area of the region lying inside x2+(y−1)2=1 and outside c2x2+y2=c2, where c=√2−1.
(4−√2)π4+1√2
(4+√2)π4−1√2
(4+√2)π4+1√2
none of these
The correct Answer is:A
Step by step video, text & image solution for Find the area of the region lying inside x^2+(y-1)^2=1 and outside c^2x^2+y^2=c^2, where c=sqrt(2)-1. by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- AREABook:FIITJEEChapter:AREAExercise:Assignment Problems (Objective) Level - II
Explore 20 Videos
- AREABook:FIITJEEChapter:AREAExercise:Comprehensions
Explore 9 Videos
- AREABook:FIITJEEChapter:AREAExercise:Exercuse 4
Explore 4 Videos
- APPLICATION OF DERIVATIVEBook:FIITJEEChapter:APPLICATION OF DERIVATIVEExercise:Numerical
Explore 3 Videos
- CIRCLEBook:FIITJEEChapter:CIRCLEExercise:Numerical Based
Explore 2 Videos
Similar Questions
Area bounded by curve y2=x and x=4 is divided into 4 equal parts by the lines x=a and y=b then a&b is
View SolutionConsider the curves C1=y−4x+x2=0 and C2=y−x2+x=0
The area of the region (in sq. units) bounded between the curves C1=0 and C2=0 is
View SolutionLet f(x) = max (x,x3)∀x∈R. Calculate the area bounded by the curves y = f(x) and the x-axis between the ordinates x = - 1 and x = 1
View Solutionf(x)=max|2siny−x| where y∈R then determine the minimum value of f(x).
View SolutionThe chords through (2,1) to the circle x2−2x+y2−2y+1=0 are bisected at the point (α,12) then value of 2α3 is ___
View SolutionThe number of such points (a+1,sqrt(3)a) where a is any integer,lying inside the region bounded by the circles x^(2)+y^(2)-2x-3=0 and x^(2)+y^(2)-2x-15=0, is
View SolutionThe area of the region defined by 1<=|x-2|+|y+1|<=2 is (a) 2 (b) 4 (c) 6 (d) non of these
View SolutionFind the area of the region lying inside x2+(y−1)2=1 and outside c2x2+y2=c2, where c=√2−1.
View SolutionThe solution of x2dydx−xy=1+cos(yx) is (A) tan(y2x)=C−12x2 (B) sec(yx)=1+Cy (C) sin(yx)=C+1y (D) y2=(C+x2)tan(yx)
View SolutionIf circles x2+y2+2x+2y+c=0 and x2+y2+2ax+2ay+c=0 where c∈R+,a≠1 are such that one circle lies inside the other, then
View SolutionIf y=c is a tangent to the circle x2+y2–2x+2y–2=0 at (1, 1), then the value of c is
View SolutionThe area (in sq. units) of the region bounded by x=−1,x=2,y=x2+1andy=2x−2 is
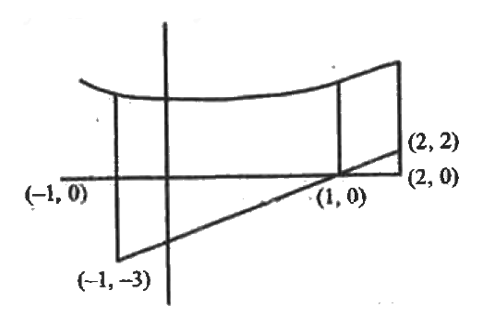
View SolutionArea ( in , sq units ) of the region outside |x|2+|y|3=1 and inside the ellipse x24+y29=1 is :
View SolutionThe number of such points (a+1,√3a), where a is any integer, lying inside the region bounded by the circles x2+y2−2x−3=0 and x2+y2−2x−15=0, is
View SolutionThe point (P+1P) (where [.] denotes the greatest integer function), lying inside the region bounded by the circle x2+y2−2x−15=0andx2+y2−2x−7=0, then :
View SolutionThe point ([P + 1], [P]), (where [.] denotes the greatest integer function) lying inside the region bounded by the circle x2+y2−2x−15=0 and x2+y2−2x−7=0, then
View Solution
