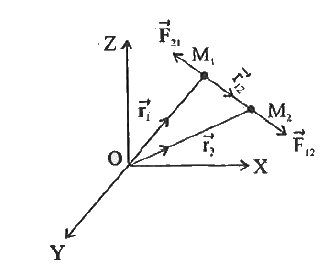
If →r1and→r2 are the position vectors of mass bodies M1andM2 then represent force between them in a vector from. Solution in Kannada
From the figure,
−→r12and→r2−→r1
By Newton's gravitational law ,
−→F12=−GM1M2r3.−→r12
i.e., −→F21=−Gm1m2r3.−→r21
where −→F21 is force on 2 due to 1
and −→r12=→r2−→r1and→r=xˆi+yˆj+zˆk
Similar Questions
Position vector of centre of two particles of masses m1 and m2 whose position vectors r1 and r2 then rcm?
View SolutionSupposing Newton's law of gravitation for gravitation forces F1 and F2 between two masses m1 and m2 at positions r1 and r2 read
where M0 is a constant of dimension of mass, r12=r1−r2 and n is a number. In such a case,
View SolutionThe distance between two particles of masses m1andm2 is r. If the distance of these particles from the centre of mass of the system are r1andr2 respectively, then show that r1=r(m2m1+m2)andr2=r(m1m1+m2)
View SolutionTwo bodies of masses m1 and m2 are separated by certain distance. If →F12 is the force on m1 due to m2 and →F21 is the force on m2 due to m1, then
View SolutionTwo bodies of masses m1 and m2 are separated by certain distance. If →F12 is the force on m1 due to m2 and →F21 is the force on m2 due to m1, then
View SolutionThe position vectors of three particles of mass m_(1)=1kg, m_(2)=2kg and m_(3)=4 are vec(r_(1))=(hat(i)+4hat(j)+hat(k))m, vec(r_(2))=(hat(i)+hat(j)+hat(k))m, and vec(r_(3))=(2hat(i)-hat(j)+2hat(k))m, respectively. Find the position vector of their centre of mass.
View Solutionमान लीजिये r1 और r2 पर स्थित दो द्रव्यमानो m1 तथा m2 के बीच गुरुत्वाकर्षण बलों F1 तथा F2 के लिए न्यूटन के गुरुत्वाकर्षण नियम को F1=−F2=−r12r312GM20(m1m2M20)n द्वारा व्यक्त किया जाता है। यहाँ M0 एक स्थिरांक है जिसकी विमा द्रव्यमान की है। r12=r1−r2 तथा n कोई संख्या है। ऐसे प्रकरण में
View Solutionदो संकेन्द्रीय गोलीय कोशों के द्रव्यमान क्रमशः m1 व m2 तथा त्रिज्यायें r1 व r2(r2>r1) हैं। इस निकाय द्वारा द्रव्यमान m3 के कण पर बल क्या होगा, यदि कण केन् से दूरी r(r1<r<r2) पर रखा हो?
View Solution
