Let A(2ˆi+3ˆj+5ˆk),B(−ˆi+3ˆj+5ˆk)andC(λˆi+5ˆj+μˆk) are vertices of a triangle and its median through A is equality inclined to the positive direction of the axes. Find the value of 2λ−μ is equal to______
The correct Answer is:2
To solve the problem, we need to find the value of 2λ−μ given the vertices of triangle A, B, and C and the condition that the median through A is equally inclined to the positive direction of the axes.
1. Identify the Coordinates of Points:
- A=(2,3,5)
- B=(−1,3,5)
- C=(λ,5,μ)
2. Find the Midpoint D of Segment BC:
The coordinates of point D (the midpoint of B and C) can be calculated as follows:
D=(xB+xC2,yB+yC2,zB+zC2)
Substituting the coordinates of B and C:
D=(−1+λ2,3+52,5+μ2)=(λ−12,4,5+μ2)
3. Determine the Direction Ratios of Line AD:
The direction ratios of line AD can be found by subtracting the coordinates of A from those of D:
Direction ratios=D−A=(λ−12−2,4−3,5+μ2−5)
Simplifying this gives:
=(λ−1−42,1,5+μ−102)=(λ−52,1,μ−52)
4. Set Up the Condition for Equal Inclination:
Since the median AD is equally inclined to the positive direction of the axes, the direction ratios must be proportional:
λ−52:1:μ−52
This implies:
λ−52=1=μ−52
5. Solve the Equations:
From the first equation:
λ−52=1⟹λ−5=2⟹λ=7
From the second equation:
1=μ−52⟹μ−5=2⟹μ=7
6. Calculate 2λ−μ:
Now substituting the values of λ and μ:
2λ−μ=2(7)−7=14−7=7
Final Answer
The value of 2λ−μ is 7.
- A=(2,3,5)
- B=(−1,3,5)
- C=(λ,5,μ)
The coordinates of point D (the midpoint of B and C) can be calculated as follows:
D=(xB+xC2,yB+yC2,zB+zC2)
Substituting the coordinates of B and C:
D=(−1+λ2,3+52,5+μ2)=(λ−12,4,5+μ2)
The direction ratios of line AD can be found by subtracting the coordinates of A from those of D:
Direction ratios=D−A=(λ−12−2,4−3,5+μ2−5)
Simplifying this gives:
=(λ−1−42,1,5+μ−102)=(λ−52,1,μ−52)
Since the median AD is equally inclined to the positive direction of the axes, the direction ratios must be proportional:
λ−52:1:μ−52
This implies:
λ−52=1=μ−52
From the first equation:
λ−52=1⟹λ−5=2⟹λ=7
From the second equation:
1=μ−52⟹μ−5=2⟹μ=7
Now substituting the values of λ and μ:
2λ−μ=2(7)−7=14−7=7
The value of 2λ−μ is 7.
Topper's Solved these Questions
Similar Questions
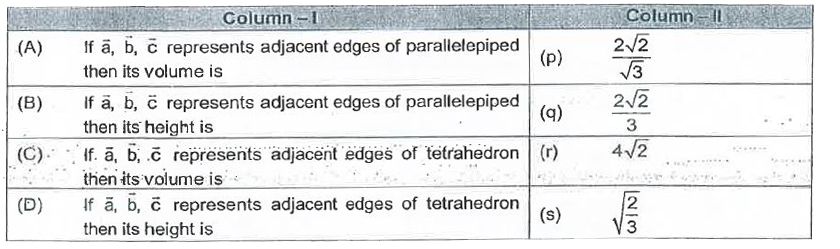
Let ¯a,¯b,¯c are the three vectors such that ∣∣¯a}=∣∣¯b∣∣=|¯c|=2 and angle between ¯aand¯bisπ/3,¯band¯cisπ/3 and ¯aand¯cπ/3.
View SolutionThe number of real roots of the equation cosecθ+secθ−√15=0 lying in [0,π] is
View SolutionThe position vectors of the points A, B, and C are ˆi+ˆj+ˆk.ˆi+5ˆj−ˆk and 2ˆi+3ˆj+5ˆk, respectively . The greatest angle of triangle ABC is -
View SolutionThe position vectors of points A,B and C are ˆi+ˆj,ˆi+5ˆj−ˆkand2ˆi+3ˆj+5ˆk, respectively the greatest angle of triangle ABC is
View SolutionThe value of 'a' for which the points A, B,C with position vectors 2ˆi−ˆj+ˆk,ˆi+2ˆk,ˆi−3ˆj−5ˆkandaˆi−3ˆj+ˆk respectively are the vertices of a right angled triangle with C=π/2, are
View SolutionLet A(2ˆi+3ˆj+5ˆk),B(−ˆi+3ˆj+2ˆk) and C(λˆi+5ˆj+μˆk) be the vertices of ΔABC and its median through A be equally inclined to the positive directions of the coordinate axds. Then, the value of 2λ−μ is
View SolutionThe position vectors of the three vertices of a triangle are (−ˆi−3ˆj+2ˆk),(5ˆi+7ˆj−5ˆk) and (2ˆi+5ˆj+6ˆk), then the position vector of the point of intersection of the medians of the triangle is -
View SolutionThe value of a, for which the points A, B and C with position vectors 2ˆi−ˆj+ˆk,ˆi−3ˆj−5ˆkandaˆi−3ˆj+ˆk respectively are the vertices of a right angled triangle with C=π2 are
View SolutionThe position vectors of the vertices of a triangle are ˆi+2ˆj+3ˆk,3ˆi−4ˆj+5ˆk and−2ˆi+3ˆj−7ˆk.Find the perimeter of the triangle
View SolutionThe position vectors of the vertices A,B,C of the triangle ABC are (ˆi+ˆj+ˆk),(ˆi+5ˆj−ˆk) and (2ˆi+3ˆj+5ˆk) respectively. Find the greatest angle of the triangle.
View SolutionTwo vertices of a triangle are at −ˆi+3ˆjand2ˆi+5ˆj and its orthocentre is at ˆi+2ˆj. Find the position vector of third vertex.
View SolutionLet A(2ˆi+3ˆj+5ˆk),B(−ˆi+3ˆj+5ˆk)andC(λˆi+5ˆj+μˆk) are vertices of a triangle and its median through A is equality inclined to the positive direction of the axes. Find the value of 2λ−μ.
View SolutionA,B ও C বিন্দুর অবস্থান ভেক্টর যথাক্রমে (ˆi+ˆj+ˆk),(ˆi+5ˆj−ˆk) এবং (2ˆi+3ˆj+5ˆk) হলে ABC ত্রিভুজের বৃহত্তম কোণ নির্ণয় করো।
View Solutionयदि सदिश ˆi−3ˆj+5ˆk और ˆi−3ˆj−aˆk बराबर सदिश हो तब a का मान होगा
View SolutionThe position vectors of points A,B and C are ˆi+ˆj,ˆi+5ˆj−ˆkand2ˆi+3ˆj+5ˆk, respectively the greatest angle of triangle ABC is
View Solution
