If (5,12)and(24,7) are the foci of a hyperbola passing through the origin, then e=√38612 (b) e=√38613 LR=1216 (d) LR=1213
e=√38612
e=√38613
LR=1216
LR=1213
The correct Answer is:A, C
Step by step video, text & image solution for If (5,12)a n d(24 ,7) are the foci of a hyperbola passing through the origin, then e=(sqrt(386))/(12) (b) e=(sqrt(386))/(13) L R=(121)/6 (d) L R=(121)/3 by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- MATHEMATICS Book:FIITJEEChapter:MATHEMATICS Exercise:PARAGRAPH BASED (MULTIPLE CHOICE)
Explore 34 Videos
- MATHEMATICS Book:FIITJEEChapter:MATHEMATICS Exercise:NUMERICAL BASED QUESTIONS
Explore 23 Videos
- MATHEMATICS Book:FIITJEEChapter:MATHEMATICS Exercise:ASSERTION REASONING
Explore 8 Videos
- MATHEMATICAL REASONING Book:FIITJEEChapter:MATHEMATICAL REASONING Exercise:ASSIGNMENT PROBLEMS (OBJECTIVE) LEVEL-2
Explore 18 Videos
- MATHEMATICS TIPSBook:FIITJEEChapter:MATHEMATICS TIPSExercise:NUMERICAL DECIMAL BASED QUESTIONS
Explore 21 Videos
Similar Questions
Two straight lines rotate about two fixed points (−a,0)and(a,o). If they start from their position of coincidence such that oen rotates at the rate double that of the other, then
The point(−a,0) always lies
View SolutionThe base AB of a triangle is 1 and height h of C from AB is less than or equal to 12. Then maximum vlaue of the 4 times the product of the altitude of the triangle is _______
View SolutionStatement1: If a line L touches the hyperbola x2−y2=a2 at A then it can also intersect the hyperbola at some other point (s).
Statement 2: Any line can intersect a second degree curve at maximum two points.
View SolutionNegation of the statement p⇒(~q∧r) is
View SolutionIf in an A.P. a7=9 and if a1a2a7 is least, then common difference is _____
View SolutionA hyperbola passes through the point P(sqrt(2),sqrt(3)) and has foci at (+-2,0) them the tangent to this hyperbola at P also passes through the point (A)(sqrt(3),sqrt(2))(B)(-sqrt(2),-sqrt(3))(C)(3sqrt(2),2sqrt(3))(D)(2sqrt(2),3sqrt(3))
View SolutionIf (5,12)and(24,7) are the foci of a hyperbola passing through the origin, then e=√38612 (b) e=√38613 LR=1216 (d) LR=1213
View SolutionThe foci of the hyperbola 3(y−1)2−4(x−2)2=12 are (0,√7) b. (−2,1−√7) c. 2,1−√7 d. (0)−√7
View SolutionIn Figure DandE are two points on BC such that BD=DE=EC Show that ar(ABD)=ar(ADE)=ar(AEC)
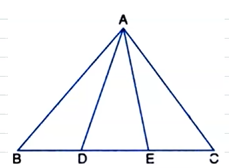
View SolutionLet R be a relation on N×N defined by (a,b) R(c,d)⇔a+d=b+c for all (a,b),(c,d)∈N×N show that: (i) (a,b)R (a,b) for all (a,b)∈N×N (ii) (a,b)R(c,d)⇒(c,d)R(a,b)for all (a,b), (c,d)∈N×N (iii) (a,b)R (c,d)and (c,d)R(e,f)⇒(a,b)R(e,f) for all (a,b), (c,d), (e,f)∈N×N
View Solution√24÷0.5+1+√18÷0.6+6=? (a) 19 (b) 13 (c) 12 (d) 15
View Solutionln(3√3)−ln(2+√3) equals (where lnx=logex)
View Solutionlog121(√14641121)= ____
View Solutionb 3 P, c 6 R, d 12 T, e 24 V, ?
View SolutionIf (5,12) and (24,7) are the foci of a hyperbola passing through the origin , then the eccentricity of the hyperbola is :
View SolutionIf (5,12), (24,7) are the foci of the hyperbola passing through origin, then its eccentricity is
View Solution
