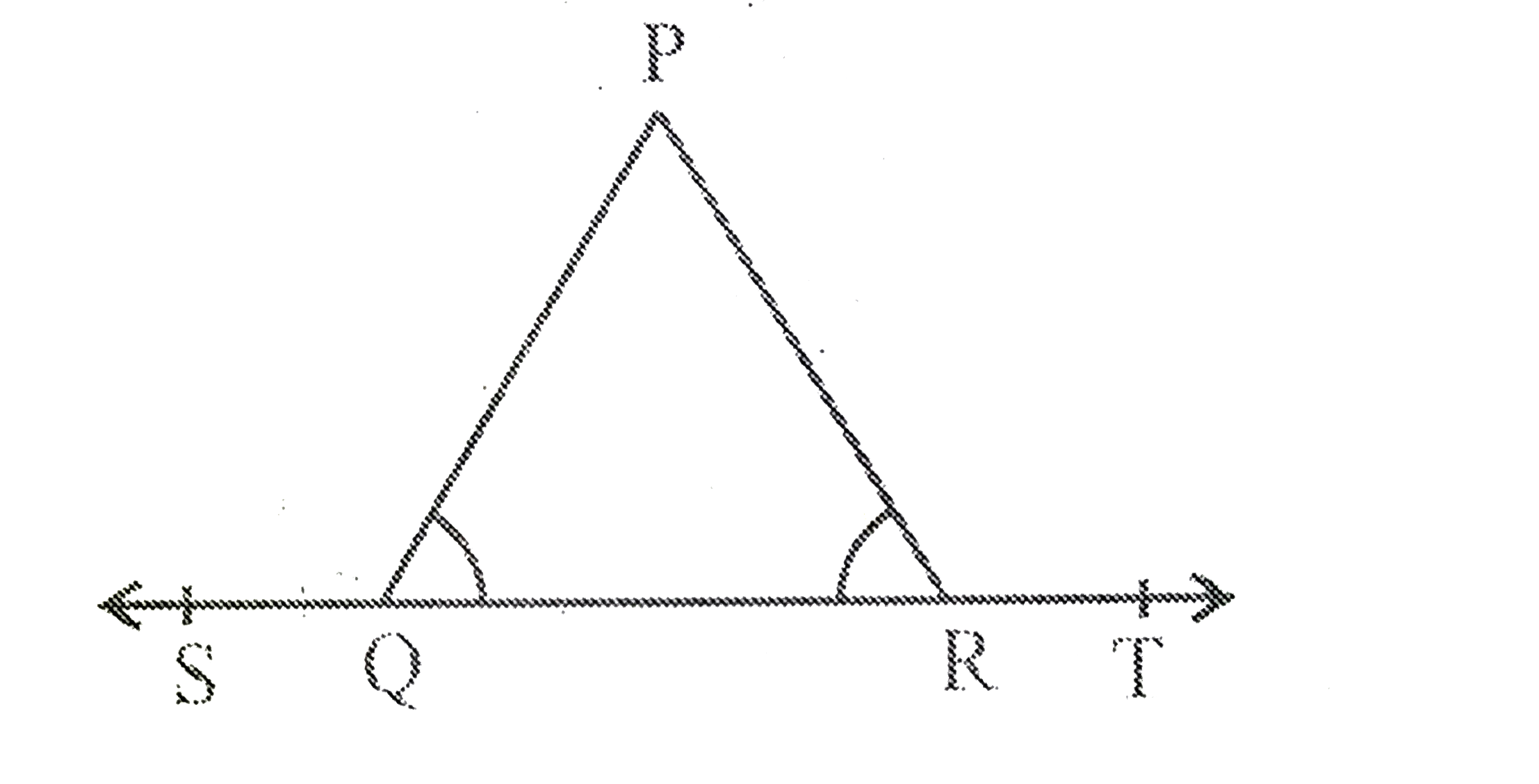
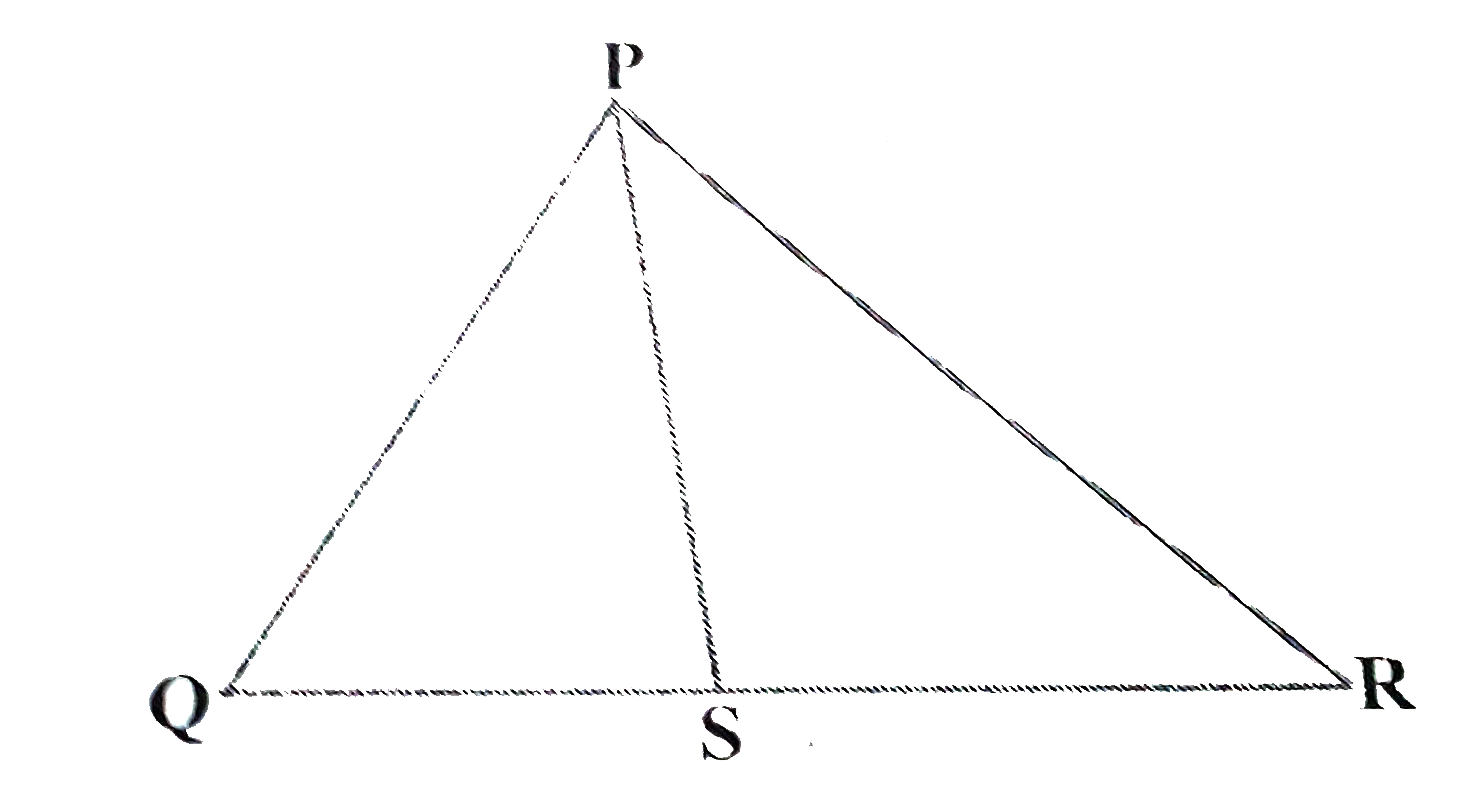
In Fig. 6.44, the side QR of PQR is produced to a point S. If the bisectors of ∠PQR and ∠PRS meet at point T, then prove that ∠QTR=12∠QPR.
Video Solution
Text Solution
In∠PQR
∠PRS=∠PQR+∠QPR(exterior angle of triangle)
12∠PRS=12∠PQR+12∠QPR
∠TRS=∠TQS+12∠QPR−(1)
In∠QTS
∠TRS=∠TQR+∠QTR−(2)
∠TQS+∠QTR=∠TQS+12∠QPR
∠QTR=12∠QPR
|
Similar Questions
Knowledge Check
P is the father of Q and R is the son of S. T is the brother of P. Q is the sister of R. How is S related to T?
Aa) BrotherBb) DaughterCc) Sister-in-lawDd) Brother-in-law
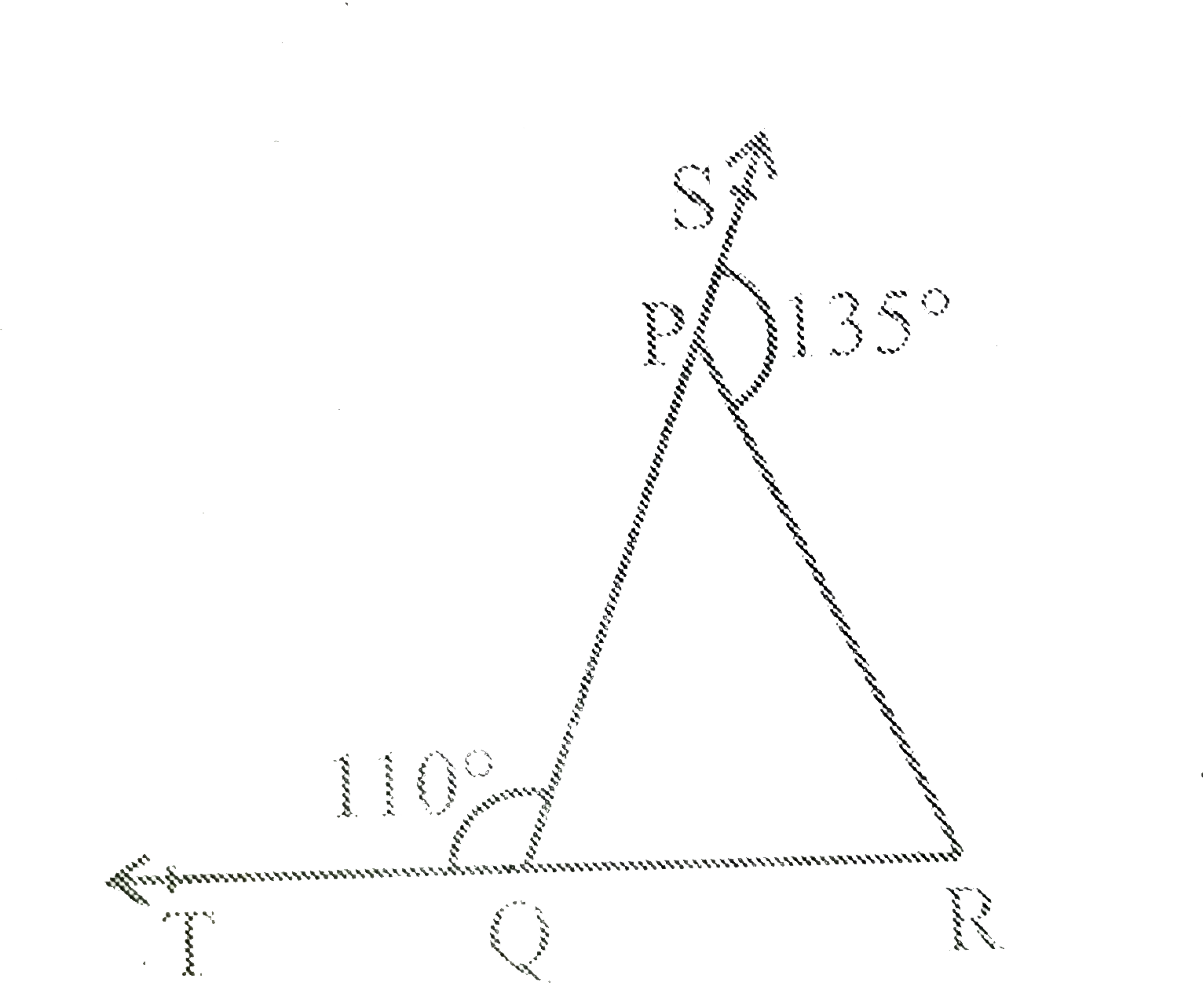
In Fig. 6.39, sides QP and RQ of ΔPQR are produced to point S and T respectively. If ∠SPR=135∘ and ∠PQT=110∘, find ∠PRQ.
View SolutionIn figure PS is the bisector of ∠QPRof ΔPQR. Prove that QSSR=PQPR.
View SolutionIn Fig. 4.90, if POS~ROQ , prove that PSQR . (FIGURE)
View SolutionIn Fig. 4.90, if PSQR , prove that POS~ROQ . (FIGURE)
View SolutionIn Fig. 6.42, if lines PQ and RS intersect at point T, such that ∠PRT=40∘,∠RPT=95∘ and ∠TSQ=75∘, find ∠SQT.

View SolutionIn ΔPQR, if PQ=QR and L,M and N are the mid-points of the sides PQ,QR and RP respectively. Prove that LN=MN.
View SolutionIn Fig 7.51, PR > PQand PS bisects ∠QPR. Prove that ∠PSR >∠PSQ.

View Solution