M द्रव्यमान का एक ब्लॉक किसी घर्षण रहित क्षेतिज सतह पर R त्रिज्या के अर्द्धवृत्ताकार मार्ग पर स्थित है। एक सर्वत्रसम (Uniform) बेलन जिसकी त्रिज्या r व द्रव्यमान m है, उच्चतम बिन्दु A से विरामावस्था से छोड़ा जाता है।
बेलन अ्द्धवृत्ताकार घर्षण रहित मार्ग पर फिसलता है। बेलन के मार्ग के निम्नतम बिन्दु B तक पहुँचने पर ब्लॉक कितनी दूरी तय कर लेगा? बेलन के मार्ग के निम्नतम बिन्दु तक पहुँचने तक ब्लॉक की गति क्या होगी? 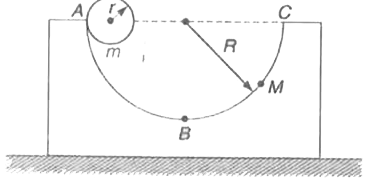
The correct Answer is:m(R−r)M+n,m√2g(R−r)M(M+n)
(a) दी गई स्थिति में (M+m) का द्रव्यमान केन्द्र क्षेतिज दिशा में गति नहीं करेगा। माना M, x दूरी बायीं ओर चलता है तब . दायी ओर (R-r-x)दूरी चलेगा। द्रव्यमान केन्द्र के क्षैतिज दिशा में गतिमान न होने का प्रतिबन्ध (Condition) होना चाहिए।
Mx=m(R−r−x)
⇒x=m(R−r)M+m
(b) माना m का वेग v1 (दायी और) तथा M का वेग v2 (बायीं और) है।
सवेग संरक्षण के नियम से mv1=Mv2...........(i)
यांत्रिक ऊर्जा संरक्षण के नियम से, mg(R−r)=12mv21+12Mv22.........(ii)
उपरोक्त समीकरणों को हल करने पर
v2=m√2g(R−r)M(M+m)
Similar Questions
यदि R त्रिज्या का एक वृत्त मूलबिंदु O से होकर जाता है तथा निर्देशांक अक्षो को A और B पर कट्टा है , तो O से रेखा AB पर डाले गए लम्ब के पाद का बिन्दुपथ है
View Solutionपरवलय y2=4ax के बिन्दु (a4,a) पर अभिलम्ब का समीकरण है
View Solutionयदि एक बल →F=3ˆi+2ˆj−4ˆk एक बिन्दु P(1,-1,2) पर कार्यरत है, तब बिन्दु Q(2, -1, 3) के सापेक्ष →F का आघूर्ण है
View Solutionबिन्दु द्रव्यमानों के समूह के कारण किसी बिन्दू पर गुरुत्वाकर्षण बल | न्यूटन के गुरुत्वाकर्षण नियम का निगमन (कैप्लर नियम से)
View Solutionघन , घनाभ तथा बेलन के क्षेत्रफल पर प्रश्न |अभ्यास प्रश्न
View SolutionRevision|बेलन का पृष्ठीय क्षेत्रफल#!#बेलन के पृष्ठीय क्षेत्रफल पर आधारित मत्वपूर्ण प्रश्न
View Solutionदो रेखाओ के मध्य कोण |बिन्दु से रेखा पर लंब
View SolutionA cylinder of radius 4.5 cm and height 12 cm just fits in another cylinder completely with their axis perpendicular. What is the radius (in cm) of second cylinder? एक बेलन जिसकी त्रिज्या 4.5 से.मी. तथा ऊँचाई 12 से.मी. है, को एक अन्य बेलन में उनके अक्षों के लम्बवत् पूरी तरह से सम्माहित किया गया है। दूसरे बेलन की त्रिज्या (से.मी. में) क्या है?
View Solution

