The sides AB and AC of ABC are product to P and Q respectively. the bisectors of exterior angles at B and C of ABC meet at O (fig.19) prove that ∠BOC=900−12∠A
∠7+∠3=∠2+∠6 ....(1) (exterior antgle theorem)
Also ∠4∠8=∠2+∠5 ....(2) (exterior angle theorem)
Adding (1) and , we get
∠7+∠3+∠4∠8=∠2+∠6+∠5+∠2
⇒∠3+∠3+∠4∠4=180∘+∠2 (∴BOandCO∠ bisectors and by using angle sum property)
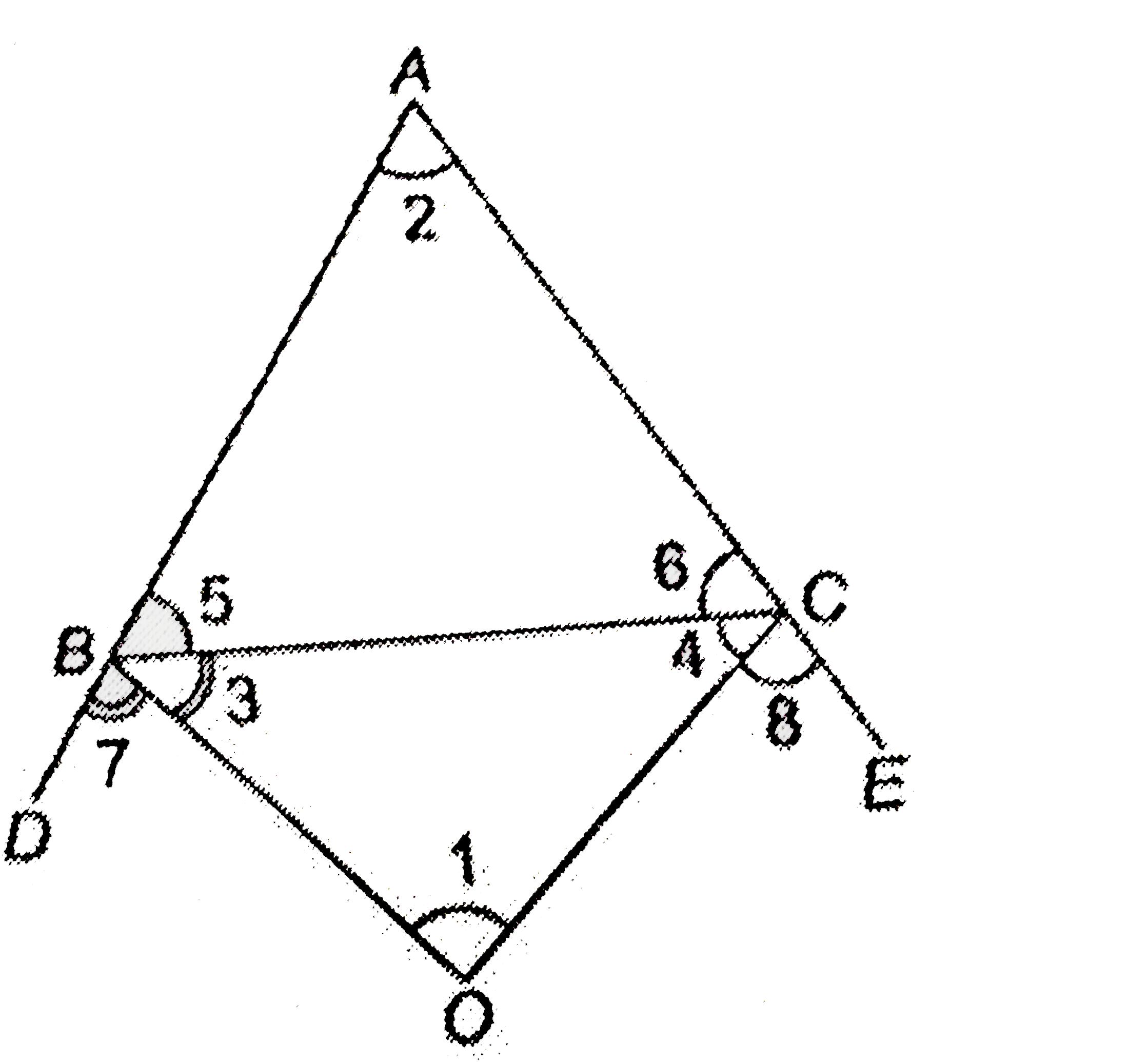
⇒2∠3+2∠4=180∘+∠2
Dividing both sides by
∴∠3+∠4=90∘+12
⇒180∘−∠1=90∘+12∠2 (by angle sum property ∠1+∠3+∠4=180∘)
⇒∠=180∘−90∘−12∠2
⇒∠1=90∘−12∠2
Topper's Solved these Questions
- LINES AND ANGLESBook:NAGEEN PRAKASHANChapter:LINES AND ANGLESExercise:Problems From NCERT/exemplar
Explore 6 Videos
- LINES AND ANGLESBook:NAGEEN PRAKASHANChapter:LINES AND ANGLESExercise:Exercise 6 A
Explore 19 Videos
- LINEAR EQUATIONS IN TWO VARIABLESBook:NAGEEN PRAKASHANChapter:LINEAR EQUATIONS IN TWO VARIABLESExercise:Revision Exercise
Explore 12 Videos
- NUMBER SYSTEMBook:NAGEEN PRAKASHANChapter:NUMBER SYSTEMExercise:Revision Exercise (short Answer Questions)
Explore 10 Videos
Similar Questions
In Fig. 6.16, if x+y=w+z, then prove that AOB is a line.
View SolutionTwo angles are in the ratio 4:5 Find the angles if they are (i) complementary (ii) supplementary to each other.
View SolutionWrite the equation of x axis.
View SolutionFind two rational numbers between −14and25.
View SolutionBO and CO are respectively the bisectors of ∠B and ∠C of ABC . AO produced meets BC at P . Show that: ABBP=AOOP (ii) ACCP=AOOP (iii) ABAC=BPPC (iv) AP is the bisector of ∠BAC .
View SolutionThe bisectors of exterior angles at B and C of ∠ABC meet at O. If ∠A=x0, then ∠BOC= 900+x02 (b) 900−x02 1800+x02 (d) 1800−x02
View SolutionThe sides AB and AC of ABC are product to P and Q respectively. the bisectors of exterior angles at B and C of ABC meet at O (fig.19) prove that ∠BOC=900−12∠A
View SolutionABC is a triangle in which ∠A=720 , the internal bisectors of angles B and C meet in O . Find the magnitude of ∠BOC.
View SolutionIn a triangle ABC,∠ABC=∠ACB and the bisectors of ∠ABC and ∠ACB intersect at O such that ∠BOC=1200. Show that ∠A=∠B=∠C=600
View SolutionIn a quadrilateral ABCD,AO andBO are the bisectors of A∠ and ∠B respectively. Prove that ∠AOB=12(∠C+∠D).
View SolutionO is any point inside a triangle ABC . The bisector of ∠AOB,∠BOC and ∠COA meet the sides AB,BC and CA in point D,EandF respectively. Show that AD⋅BE⋅CF=DB⋅EC⋅FA
View SolutionBO and CO are respectively the bisectors of ∠B and ∠C of ABC . AO produced meets BC at P . Show that: ABBP=AOOP (ii) ACCP=AOOP (iii) ABAC=BPPC (iv) AP is the bisector of ∠BAC .
View SolutionIn a quadrilateral ABCD , ∠B=90o , AD2=AB2+BC2+CD2 , prove that ∠ACD=90o
View SolutionIn Figure, given that ∠AOC=∠ACO and ∠BOD=∠BDO. Prove that AC∣∣DB
View SolutionIn a triangle ABC, ∠ABC= ∠ACB and the bisectors of ∠ABC and ∠ACB intersect at O such that ∠BOC=1200. Show that ∠A=∠B=∠C=600 .
View SolutionIn a triangle ABC, the internal bisectors of ∠B and ∠C meet at P and the external bisectors of ∠B and ∠C meet at Q . Prove that ∠BPC+ ∠BQC=1800
View Solution