दो सरल आवर्त गतियों कि निरूपित करने वाले समीकरण, y1=10sin(3πt+π/4) तथा y2=5(sin3πt+√3cos3πt) है , उनके आयामों का अनुपात . . . . है
The correct Answer is:1:1
प्रश्नानुसार, A1=10,A2 के लिए
y2=5sin3πt+5√3cos3πt=5sin3πt+5√3sin(3πt+π2)
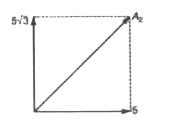
अर्थात् दोनों फलन π2 का कलान्तर रखते है , अतः परिणामी आयाम A2 को सदिश विधि द्वारा निम्न प्रकार प्राप्त किया जा सकता है :
A2√(5)2+(5√3)2=10∴A1A2=1010=1
समान प्रश्न
The equation of the two-wave deduction is y_(1) = 10 sin (3 pi t + pi/3), y_(2) = 5 (sin 3pi t + sqrt(3) cos 3 pi t) The ratio of their dimensions will be
View SolutionTwo SHM are represented by the equations y_(1) = 10 sin(3pi t + pi//4) and y_(2) = 5[sin 3pi t + sqrt(3) cos 3pi t] . Their amplitudes are in the ratio
View SolutionIf two SHMs are represented by equations y1= 4 sin[3πt + (π/3)], y2= 4 [sin(3πt) +√3 cos (3πt)], then the ratio of their amplitudes is
View SolutionThe S.H.M.s of two particles are given by y_(1)=10 "sin" [2pi t +(pi)/(6)] " and " y_(2) =5["sin" 2pi t + sqrt(3) "cos" 2 pi t] The ratio of their amplitudes is
View SolutionIf two SHMs are repersented by y1=10sin(4π+π/2) and y2=5(sin2πt+√8cos2πt), compare their amplitudes .
View SolutionThe equation of displacement of two waves are given as
y1=10sin(3πt+π3),y2=5[sin3πt+√3cos3πt]
Then what is the ratio of their amplitudes
View SolutionThe equation of displacement of two waves are given as y_(1) = 10 sin( 3 pi t + (pi)/(3)) , y_(2) = 5 [ sin 3 pi t + sqrt(3) cos 3 pi t] Then what is the ratio of their amplitudes
View SolutionIf two SHMs are represented by equations y_1 = 4 sin[3 pi t + ( pi /3)], y_2 = 4 [sin(3 pi t) + sqrt 3 cos (3 pi t)], then the ratio of their amplitudes is
View Solution
