चित्र में दिखाये गये दो सदिशों →A और →B के बीच का कोण θ है। इनके परिणामी सदिश का परिमाण तथा दिशा उनके परिमाणों तथा θ के पद मे निकालिए। 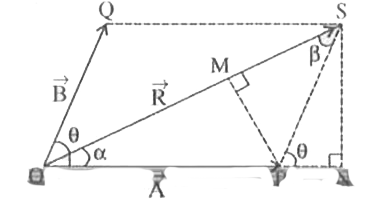
चित्र के अनुसार माना −−→OP तथा −−→OQ दो सदिशों →A तथा →B को व्यक्त करते हैं जिसके बीच का कोण θ है। तब सदिश योग के समांतर चतुर्भुज नियम द्वारा हमें परिणामी सदिश →R प्राप्त होगा, जिसे चित्र में −−→OS द्वारा दिखाया गया है।
→R=→A+→B
चित्र में SN⊥OP और PM⊥OS
∴OS2=ON2+SN2
लेकिन ON=OP+PN=A+Bcosθ
∵cosθ=PNSP∴PN=Bcosθ
sinθ=SNSP=SNB SN=Bsinθ
∴OS2=(A+Bcosθ)2+(Bsinθ)2
अथवा R2=A2+2ABcosθ+B2cos2θ+B2sin2θ
R2=A2+2ABcosθ+B2(cos2θ+sin2θ)
R2=A2+2ABcosθ+B2×1 sin2θ+cos2θ=1
⇒R2=A2+B2+2ABcosθ
=R=√A2+B2+2ABcosθ………1
ΔOSN में SN=PSsinθ=Bsinθ
अतएव Rsinα=Bsinθ∴Rsinθ=Bsinα…….2
इसी प्रकार PM=Asinα=Bsinβ
अथवा Asinβ=Bsinα……..3
समीकरण 2 तथा 3 को शामिल करने पर
Rsinθ=Asinβ=Bsinα………4
समीकरण 4 को ज्या नियम कहते हैं।
समकोण त्रिभुज ONS से
tanα=NSON=NSOP+PN
=BsinθA+Bcosθ
⇒tanα=BsinθA+Bcosθ…….5
Similar Questions
यदि →a,→b,→c समान परिमाण के परस्पर लम्ब सदिश हो तो सिद्ध कीजिए कि सदिश →a+→b+→c सदिशों →a,→b और →c के साथ बराबर कोण बनाता है।
View Solutionसदिश →a=ˆi+ˆj+ˆk का सदिशों →b=2ˆi+4ˆj−5ˆk तथा →c=λˆi+2ˆj+3ˆk के योगफल की दशा में एक मात्रक सदिश के साथ अदिश गुणनफल 1 के बराबर है का मान ज्ञात कीजिए तथा →b+→c की दशा में एक मात्रक सदिश ज्ञात कीजिए।
View Solution→a और →b के मध्य कोण 5π6 है तथा →a तथा →b पर प्रक्षेप −9√3 है , तो |→a| है -
View Solutionयदि →a=ˆi+2ˆj+2ˆk,∣∣→b∣∣=5 और →a तथा→b के बीच कोण π6 है , तब दोनों भुजाओं के रूप में इन दो सदिशों के द्वारा बनने वाले त्रिभुज का क्षेत्रफल है -
View Solutionकोई रेखा x-अक्ष और y-से साथ क्रमशः 60∘ तथा 45∘ के कोण बनाती है। इनके द्वारा घनत्व दिशा में z-अक्ष के साथ कितना कोण बनेगा ?
View Solutionयदि सदिश →a,→b तथा →c के लंबवत है, |→a|=2,∣∣→b∣∣=3,|→c|=4 और →b तथा →c के बिच का कोण 2π3 है। तब [→a→b→c] बराबर है
View Solutionयदि a तथा b इकाई सदिश हैं तथा θ इनके बीच का कोण है। तब ∣∣ˆa+ˆb∣∣<1 यदि
View Solutionभौतिक राशियो का वर्गीकरण #!#सदिश राशियो के प्रकार #!#सदिश राशियो का निरूपण व उनके मध्य कोण
View Solution

