A starts from rest, with uniform acceleration a. The acceleration of the body as function of time t is given by the equation a = pt, where p is a constant, then the displacement of the particle in the time interval t = 0 to t=t1 will be
12pt31
13pt21
12pt21
12pt31
The correct Answer is:D
Integrate twice to convert a-t equation into s-t equation.
∵a=υt⇒υ=at
⇒∫dυ∫a.dt→υ∫pt.dt=pt22
∵s=υ×t⇒ds=υdt
⇒∫ds=∫υdt⇒s=16pt3
Similar Questions
समय t पर, त्वरण f से x-अक्ष पर गति करते कण का समीकरण f=f0(1−1T) है। जहाँ f0 तथ T नियतांक हैं। समय t = 0 पर कण विरामावस्था में है। समयान्तर, t = 0 तथा वह क्षण, जब f = 0 है, तब मध्य कण का वेग vx है
View SolutionIf acceleration (a)=2t+1, where t is time.Find displacement as function of time,Given that initally particle is at rest
View SolutionStarting from rest a body moves at first with constant acceleration a. Then it moves with a uniform velocity and finally comes to rest with a constant retardation a. If the displacement is s and time taken is t, prove that the body was in motion with uniform velocity for a time interval of sqrt(t^(2)-4s//a).
View SolutionA body accelerates from rest with a uniform acceleration a for time t. The uncertainty in a is 8% and the uncertainty in t is 4% . The uncertainty in speed is :
View SolutionA body starting from rest moves with constant acceleration 'a'. This acceleration is a pr where p is a constant. What is the displacement of particle in a time interval=0 to t = t1 ?
View SolutionA graph of acceleration versus time of a particle starting from rest at t =0 is shown. The speed of the particle at t=14 second is
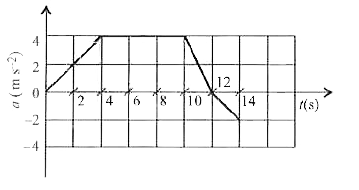
View SolutionThe acceleration of a particle varie with time as shown in the figure Find the displacement of the particle in the interval from 1 = 2s to t = 4s Assume that v = 0 at t=0
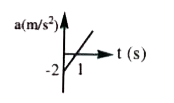
View SolutionA particle accelerates from rest with uniform acceleration alpha then decelerates to rest witha constant deceleration beta . Find total displacement. Given time is T
View Solution

