Self - inductance 0.8×10−4H of a uniformly wound solenoid, having resistance 3 Ω is broken up into two indentical coils. Those coils are connected in series across a 6 V battery of negligible resistance. Find time constant and steady state current.
For a solenoid, self inductance is given by
L=μ0N2πr2l
where, r = radius of colenoid, l = length of solenoid,
N = number of turns
are we know that, resistance is given by
R=ρlA=ρN2πrA
So, on breaking it into two parts, now inductance and resistance is given as
N'=N2,l'=l2⇒L'=μ0(N/2)2πr2l/2=L2
R'=ρ(N/2)×2πrA=R
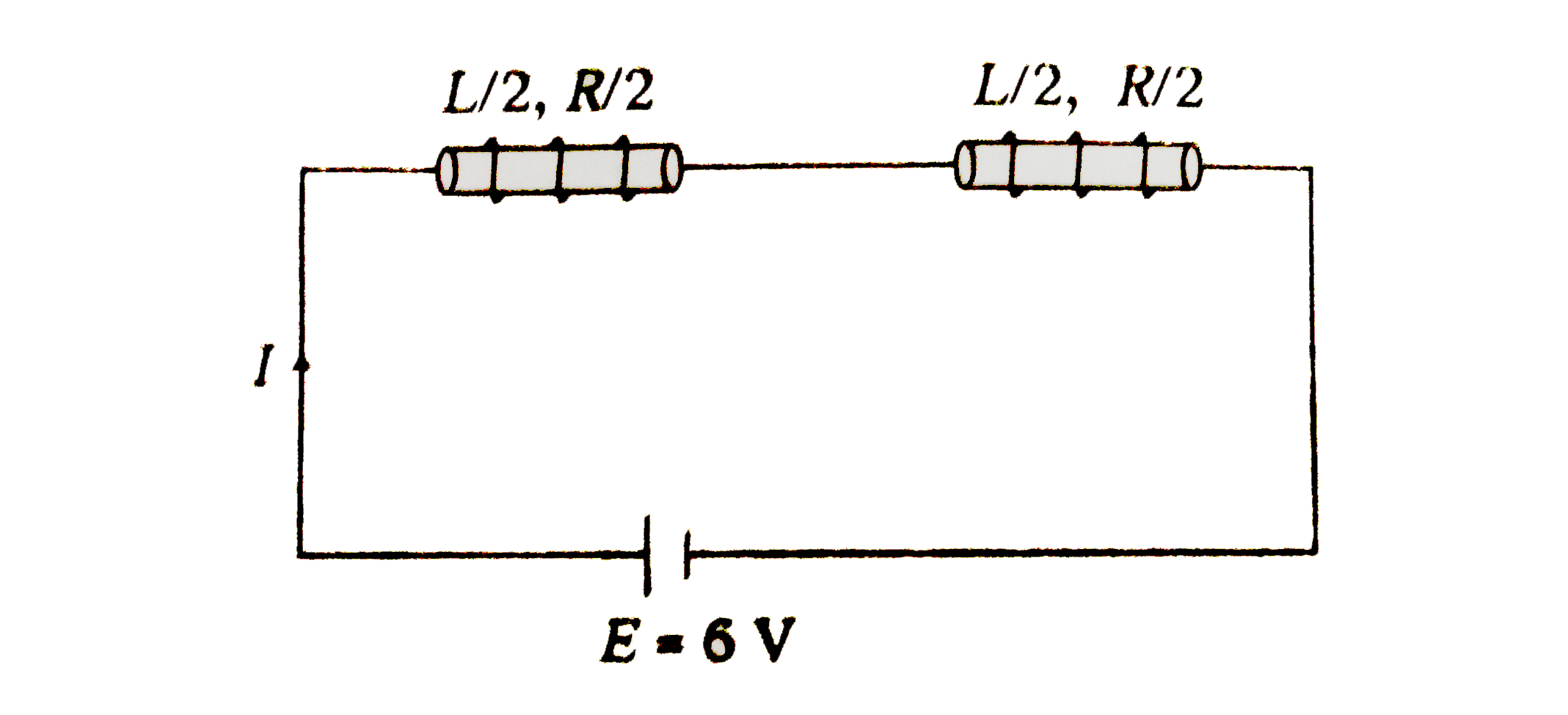
So, the equivalent inductance, Leq=L1+L2
=L/2+L/2=L
and eqivalent resistance, Req=R1+R2=R/2+R/2=R
So, the time constant,
τ=LeqReq=0.8×10−43=0.267×10−4s
and current, I=EReq=ER=63=2A
Similar Questions
A uniform wound solenoidal coil of self inductance 1.8×10−4 henry and resistance 6 ohm is broken up into two identical coils. These identical coils are then connected in parallel across a 15-volt battery of negligible resistance. The time constant for the current in the circuit is.......seconds and the steady state current through the battery is ..............amperes.
View SolutionA uniform wound solenoid coil of self inductance 1.8×10−4H and resistance ohm is broken into two identical coils. These indentical coils are connected in parallel across a 12 V battery of negligible resistance. Calculate the steady state current through the battery and time constant of the circuit.
View Solution
Knowledge Check
A uniformly wound solenoid coil of self inductance 1.8×10−4H and resistance 6Ω is broken up into two identical coils. These identical coils are then connected in parallel across a 12V battery of negligible resistance. The time constant and steady state current will be
A10μsec,6AB10μsec,8AC30μsec,6AD30μsec,8AA uniformly wound solenoid coil of slf inductnace 4 mH and resistance 12Ω is broken int two parts. These two coil are connected in parallel across is 12V battery. The steady current through battery is
A1AB2AC4AD8ATwo coils of resistances 3Ωand6Ω are connected in series across a battery of emf12V. Find the electrical energy consumed in 1 minute in each resistance when these are connected in series.
A500 J, 500 JB320 J, 640 JC320 J, 320 JDNone of these
A solenoid having a resistance of 5Ω and self-inductance of 4H is connected to a battery of emf 10V and negligible resistance. After how long will the current in it rise to 1A ?
View SolutionTwo resistors 4Ωand6Ω connected in parallel. The combination is connected across a 6V battery of negligible resistance. Calculate
(a) the current through the battery
(b) current through each resistor.
View SolutionAn inductor coil carries a steady state current of 2.0 A when connected across an ideal battery of emf 4.0 V. if its inductance is 1.0 H, find the time constant of the circuit.
View SolutionA 5 V battery of negligible internal resistance is connected across a 200 V battery and a resistance of 39Ω as shown in the figure. Find the value of the current.

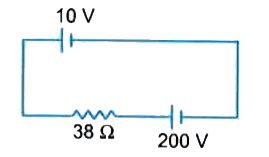
View SolutionA 10 V battery of negligible internal resistance is connected across a 200 V battery and a resistance of 38 Ω as shown in the Fig. Find the value of the current in circuit.
View Solution
