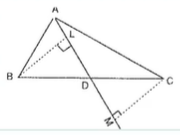
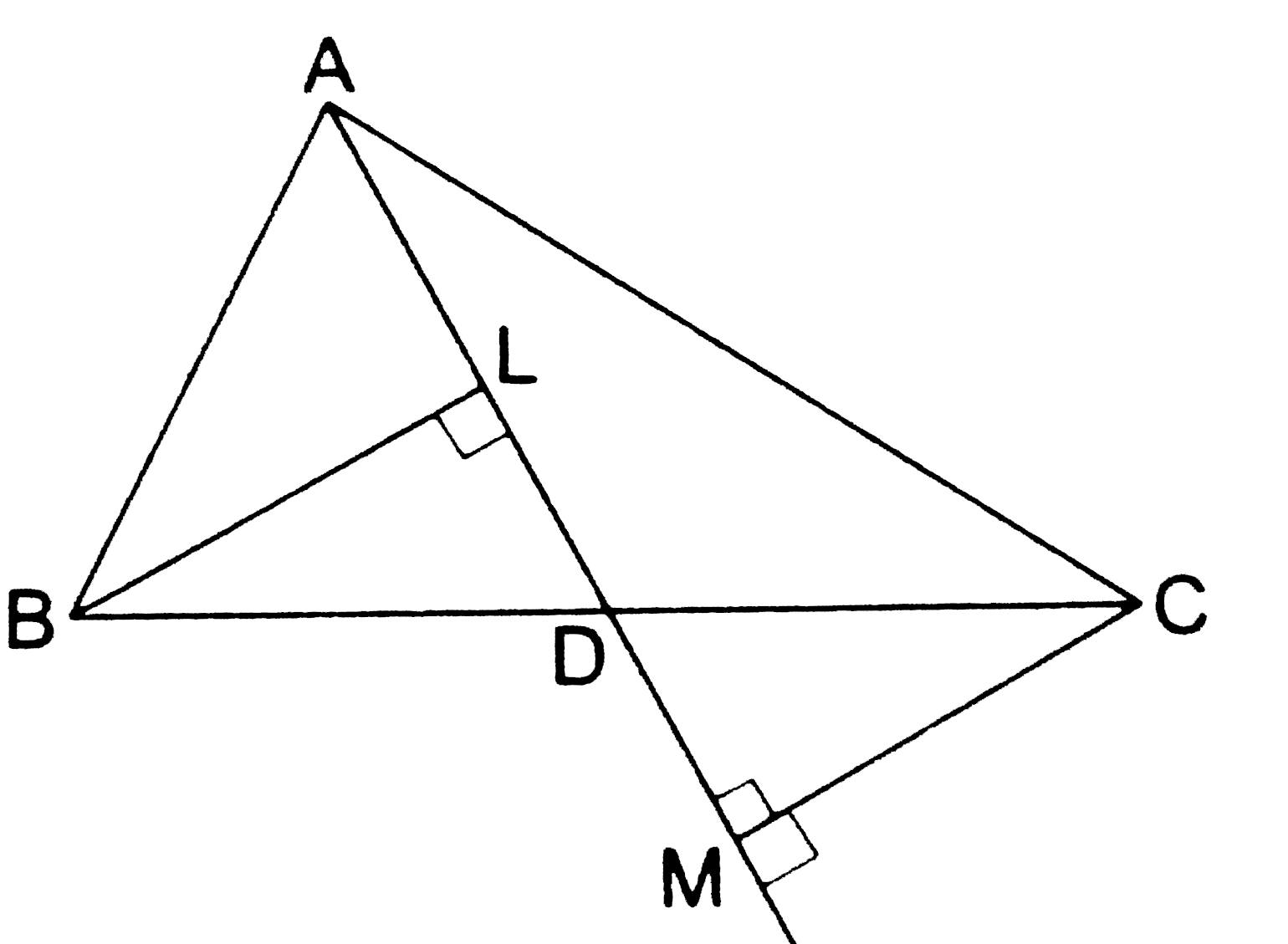
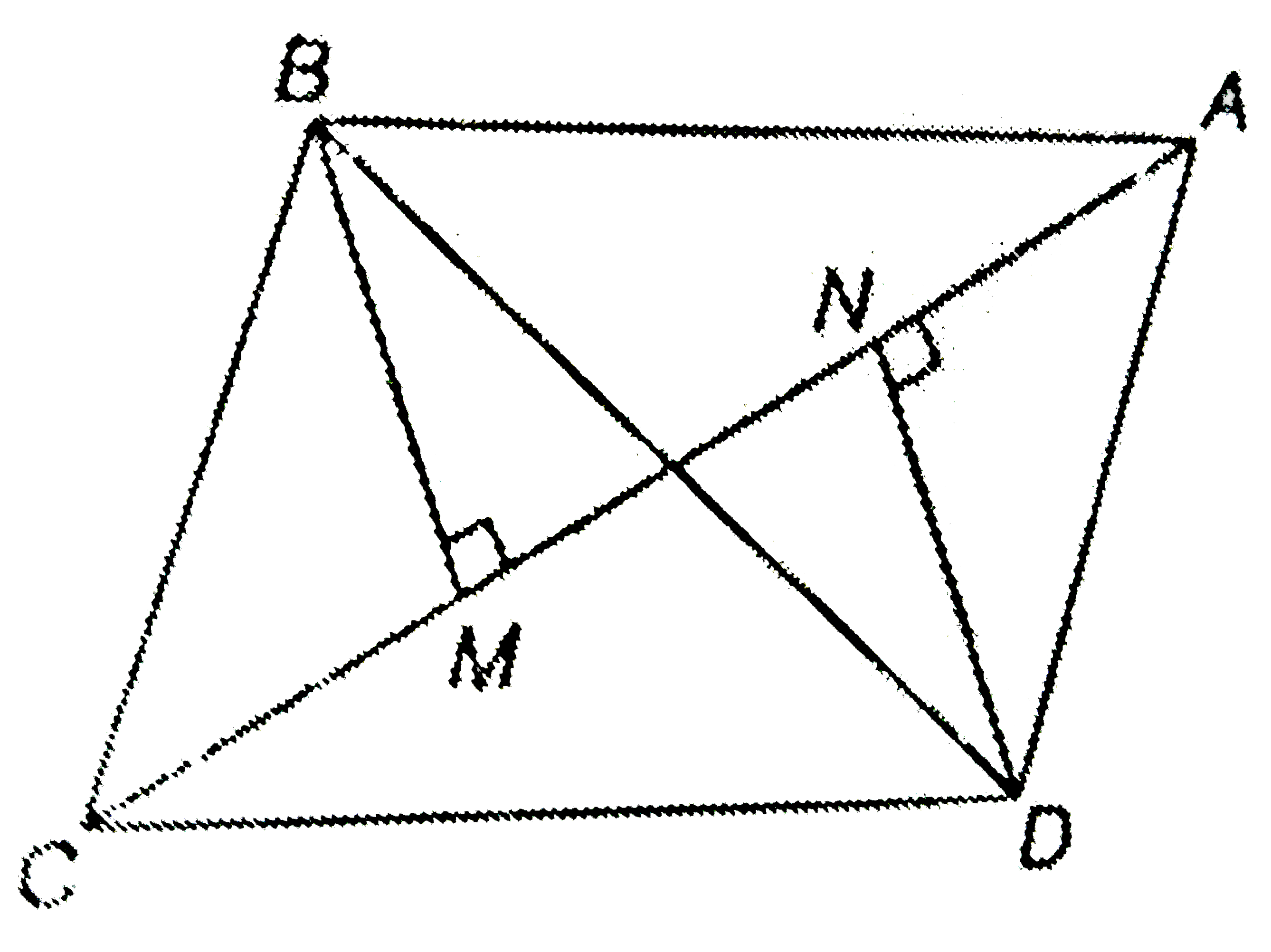
In the adjoining figure, D is the mid-point of BC. If BM and CN are perpendiculars from B and C respectively on AD and AD produced, then prove that BM = CN.

Video Solution
Text Solution
Given : ΔABC in which D is the mid-point of BC, BM⊥AD and CN⊥AD
To Prove : BM=CN
Proof : In ΔBMD and ΔCND,
∵⎧⎪⎨⎪⎩∠BMD=∠CND(each 90∘, given)∠BDM=∠CDN(vertically opposite angle)BD=CD(given)
∵ΔBMD≅ΔCND (AAS)
⇒BM=CN (c.p.c.t) Hence Proverd.
|
Similar Questions
Knowledge Check
In the adjoining figure, AD = 2AB = a. If P is the mid-point of AD, then area of the shaded region is
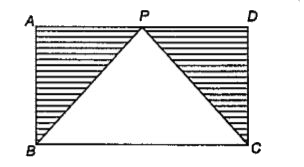 Aa2Ba22Ca23Da24
Aa2Ba22Ca23Da24In the adjoining figure, AD = 2AB = a. If P is the mid-point of AD, then area of the shaded region is
 Aa2Ba22Ca23Da24
Aa2Ba22Ca23Da24
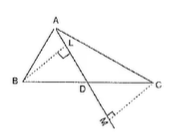
In the adjoining figure, AD is a median of ΔABC. If BL and CM are drawn perpendiculars on AD and AD produced, prove that BL = CM.
View SolutionIn the adjoining figure, BM and DN are the perpendiculars from B and D respectively to AC such that BM = DN. Prove that BO = OD.
View SolutionIn Figure, ABCD is a rectangle. BM and DN are perpendicular from B and D respectively on AC . Prove that MBC≅DNA (ii) BM=DN
View SolutionIn an adjoining figure, ABCD is a rectangle, BM and DN are perpendicular from B and D on AC (i) Is ΔBMC=ΔDNA
View SolutionIn a ΔABC, if D is the mid point of BC and AD is perpendicular to AC, then cosB=
View SolutionIn the adjoining figure D, E and F are the mid - points of the sides BC, AC and AB respectively to triangle. Show that ∠EDF=∠A, ∠DEF=∠B and ∠DFE=∠C:

View Solution