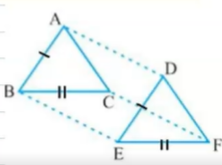
XY is a line parallel to side BC of a triangle ABC. If BE ∣∣ ACand CF ∣∣ ABmeet XY at E and F respectively, show that ar (ABE) = ar (ACF)
Draw prependiculars GM and DN from C and D respectively to AB.
Given that
area of ΔAOD= area of ΔBOC
Adding area of ΔAOB on both sides.
area of ΔAOD+ area of ΔAOB
= area of ΔBOC+ area of ΔAOB
⇒ area of ΔABD= area of ΔABC
⇒ area of ΔABD= area of ΔABC
⇒12×AB×DN=12×AB×CM
⇒DN=CM

∴DC∣∣AB
(perpendicular distancce between two parallel lines area always same)
∴□ABCD is a trapezium.
Topper's Solved these Questions
- AREA OF PARALLELOGRAMS AND TRIANGLESBOOK - NAGEEN PRAKASHANCHAPTER - AREA OF PARALLELOGRAMS AND TRIANGLESEXERCISE - Problems From NCERT/exemplar
12 Videos
- AREA OF PARALLELOGRAMS AND TRIANGLESBOOK - NAGEEN PRAKASHANCHAPTER - AREA OF PARALLELOGRAMS AND TRIANGLESEXERCISE - Exercise
34 Videos
- CIRCLE BOOK - NAGEEN PRAKASHANCHAPTER - CIRCLE EXERCISE - Revision Exercise (long Answer Questions )
5 Videos
Similar Questions
If E, F, G and H are respectively the mid-points of the sides of a parallelogram ABCD, Show that ar(EFGH)=12AR (ABCD)
View SolutionThe base of a parallelogram is 3 times of its corresponding height. If the area of the parallelogram is 48cm2, then find the base and the corresponding height of the parallelogram.
View SolutionAB and CD are two chords of a circle such that AB=6 cm, CD=12 cm and ABCD. If the distance between AB and CD is 3 cm, find the radius of the circle.
View SolutionXY is a line parallel to side BC of a triangle ABC. If BE ∣∣ ACand CF ∣∣ ABmeet XY at E and F respectively, show that ar (ABE) = ar (ACF)
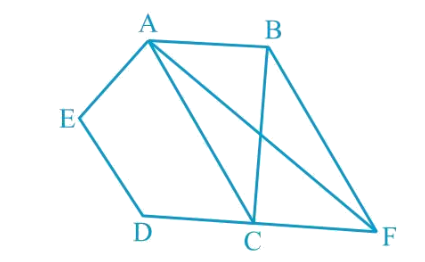
View SolutionIn Figure, ABCDE is a pentagon. A line through B parallel to AC meets DC produced at F. Show that ar(ACB)=ar(ACF) (ii) ar(AEDF)=ar(ABCDE)
View SolutionXY isa line parallel to side BC of ABC.BEA and CFAB meet XY in E and F respectively.Show that ar(ABE)=ar(ACF).
View SolutionIf ABC and DEF are two triangles such that AB, BC are respectively equal and parallel to DE, EF, then show that Quadrilateral ABED is a parallelogram Quadrilateral BCFE is a parallelogram AC=DF (iv) ABC ≅ DEF
View SolutionIn Figure, ABCDE is a pentagon. A line through B parallel to AC meets DC produced at F. Show that: ar (ACB)=ar (ACF) ar (AEDF)=ar (ABCDE)
View SolutionXY is a line parallel to side BC of a triangle ABC. If BE∣∣AC and CF ∣∣ AB meet XY at E and F respectively, show that ar (ABE) = ar (ACF)
View SolutionIf D,EandF are three points on the sides BC,CAandAB, respectively, of a triangle ABC show that the BDCD=CEAE=AFBF=−1
View SolutionIn a parallelogram ABCD,E,F are any two points on the sides AB and BC respectively. Show that ar(△ADF)=ar(△DCE).
View SolutionIn Figure, ABCDE is a pentagon. A line through B parallel to AC meets DC produced at F. Show that: (i) ar(△ACB)=ar(△ACF) (ii) ar(quadrilateralAEDF)=ar(ABCDE)
View SolutionXY is a line parallel to side BC of triangle ABC.BEllACandCF ll ABmeetXY∈EandFrespectively.Showtˆa r( A B E)=a r( A C F)dot
View SolutionIf ABC and DEF are two triangles such that ABDE=BCEF=CAFD=34 , then write Area (ABC):Area(DEF) .
View SolutionIf ABC and DEF are two triangles such that ABDE=BCEF=CAFD=25 , then Area(ABC):Area(DEF)=
View SolutionIf ΔABC~ΔDEF such that BC=3cm , EF=4cm and ar(ABC)=54cm2 , then ar(DEF)=
View Solution
