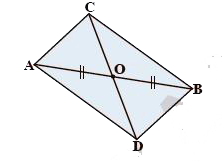
In Fig. 9.24, ABC and ABD are two triangles on the same base AB. If line- segment CD is bisected by AB at O, show that
Given, ABC and ABD are two triangle on the same base AB.
The line segment CD is bisected by AB at O. (.:OC=OD)
In ΔACD, we have
OC=OD (given)
∴AO is the median.
Since, the median divides a triangle in two triangles of equal areas.
∴ar(ΔAOC)=ar(ΔAOD)...(1)
Similarly, in ΔBCD, ar(ΔBOC)=ar(ΔBOD)...(2)
On adding (1) and (2), we get
ar(ΔAOC)+ar(ΔBOC)=ar(ΔAOD)+ar(ΔBOD)
⇒ar(ΔABC)=ar(ABD)
Similar Questions
In the given figure, ABC and ABD are two triangles on the same base AB . If line - segment CD is bisected by AB at O, show that ar (ABC) = ar (ABD)
View SolutionTriangles on the map /_\ABC And /_\ABD Single earths are above AB. If the CD line segment intersects the overline (AB) at O equilaterally (/_\ABC) Y || = (/_\ABD) Why || Show that.
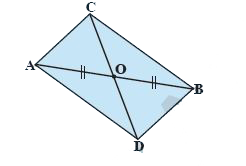
View SolutionIn the figure, ΔABC and ΔABD are two triangles on the same base AB. If line segment CD is bisected by ¯¯¯¯¯¯AB at O, show that ar (ΔABC)=ar(ΔABD).
View SolutionIn the figure, ΔABC and ΔABD are two triangles on the same base AB. If line segment CD is bisected by ¯¯¯¯¯¯AB at O, show that ar (ΔABC)=ar(ΔABD).

View SolutionIn the figure, ΔABC and ΔABD are two triangles on the same base AB. If line segment CD is bisected by ¯¯¯¯¯¯AB at O, show that ar (ΔABC)=ar(ΔABD).
View SolutionAD and BC are equal perpendiculars to a line segment AB (see Fig. 7.18). Show that CD bisects AB.

View SolutionIn Fig. 9.24, ABC and ABD are two triangles on the same base AB. If line- segment CD is bisected by AB at O, show that
View Solutionआकृति में, ABC और ABD एक ही आधार AB पर स्थित दो त्रिभुज हैं। यदि रेखाखंड CD रेखाखंड AB द्वारा 0 पर समद्विभाजित होता है, तो दर्शाइए कि क्षेत्रफल (ΔABC) = क्षेत्रफल (ΔABD) है।

View Solution