Give example of polynomials p(x),g(x),q(x) and r(x) which satisfy the division algorithm and
(i) degp(x)=deg q(x)
(ii) deg q(x)=deg r(x)
(iii) deg r(x)=0
Text Solution
(i) Let p(x)=2x2−2x+14 and g(x)=2

∴ q(x)=x2−x+7 and r(x)=0
Now, degp(x)=degq(x)
(ii) Let p(x)=x3+x2+x+1 and g(x)=x2−1
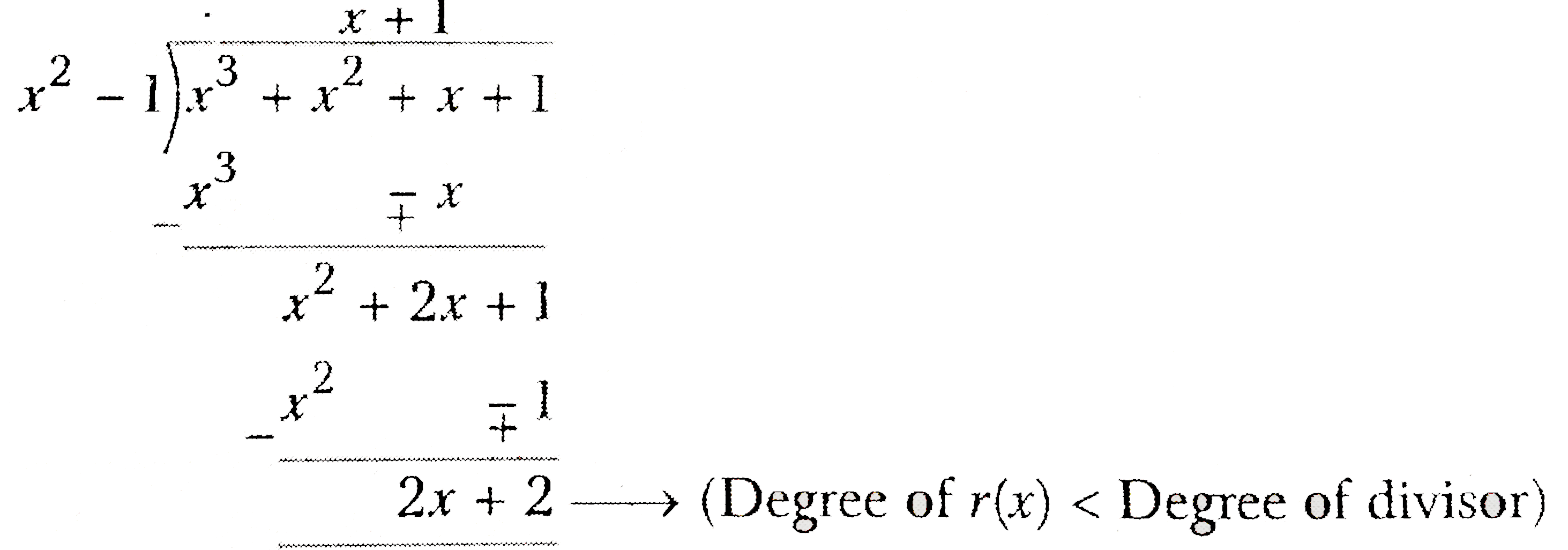
∴ q(x)=x+1 and r(x)=2x+2
⇒degq(x)=degr(x)
(iii) Let p(x)=x3+2x2−x+2 and g(x)x2−1

∴ q(x)=x+2 and r(x)=4
Now degr(x)=0
|
Similar Questions
Knowledge Check
If deg (f(x))=5 & deg (g(x))=4 then deg [f(x)-g(x)] is
A5B4C1D9Assertion : 3x2+x−1=(x+1)(3x−2)+1 .
Reason : If p(x) and g(x) are two polynomials such that degree of p(x)≥ degree of g(x) and g(x)≥0 then we can find polynomials q(x) and r(x) such that p(x)=g(x).q(x)+r(x), where r(x)=0 or degree of r(x)< degree of g(x) .AIf both assertion and reason are true and reason is the correct explanation of assertion .BIf both assertion and reason are true but reason is not the correct explanation of assertion .CIf assertion is true but reason is false .DIf assertion is false but reason is true .On dividing a polynomial p(x) by a non-zero polynomial q(x), let g(x) be the quotient and r(x) be the remainder then =q(x)⋅g(x)+r(x),where
Ar(x)=0 alwaysBdeg r(x)> deg q(x) alwaysCeither r(x)=0 or deg r(x)< deg q(x)Dr(x)=g(x)
Give examples of polynomials p(x), g(x), 9(x) and r(x), which satisfy the division algorithm and
deg r(x)=0
View SolutionGive examples of polynomials p(x), g(x), 9(x) and r(x), which satisfy the division algorithm and
deg q(x)= deg r(x)
View SolutionGive an example of polynomials f(x), g(x), q(x) and r(x) satisfying f(x)=g(x).q(x)+r(x) , where degree r(x)=0 .
View SolutionGive an example of polynomials f(x), g(x), q(x) and r(x) satisfying f(x)=g(x).q(x)+r(x) , where degree r(x)=0 .
View SolutionApply division algorithm to find the quotient q(x) and remainder r(x) on dividing f(x)=x3−6x2+11x−6 by g(x)=x2+x+1
View Solution
