The hypotenuse of a right angled triangle has its ends at the points (1, 3) and ( 4, 1) . Find the equation of the legs (perpendicular sides) of the triangle.
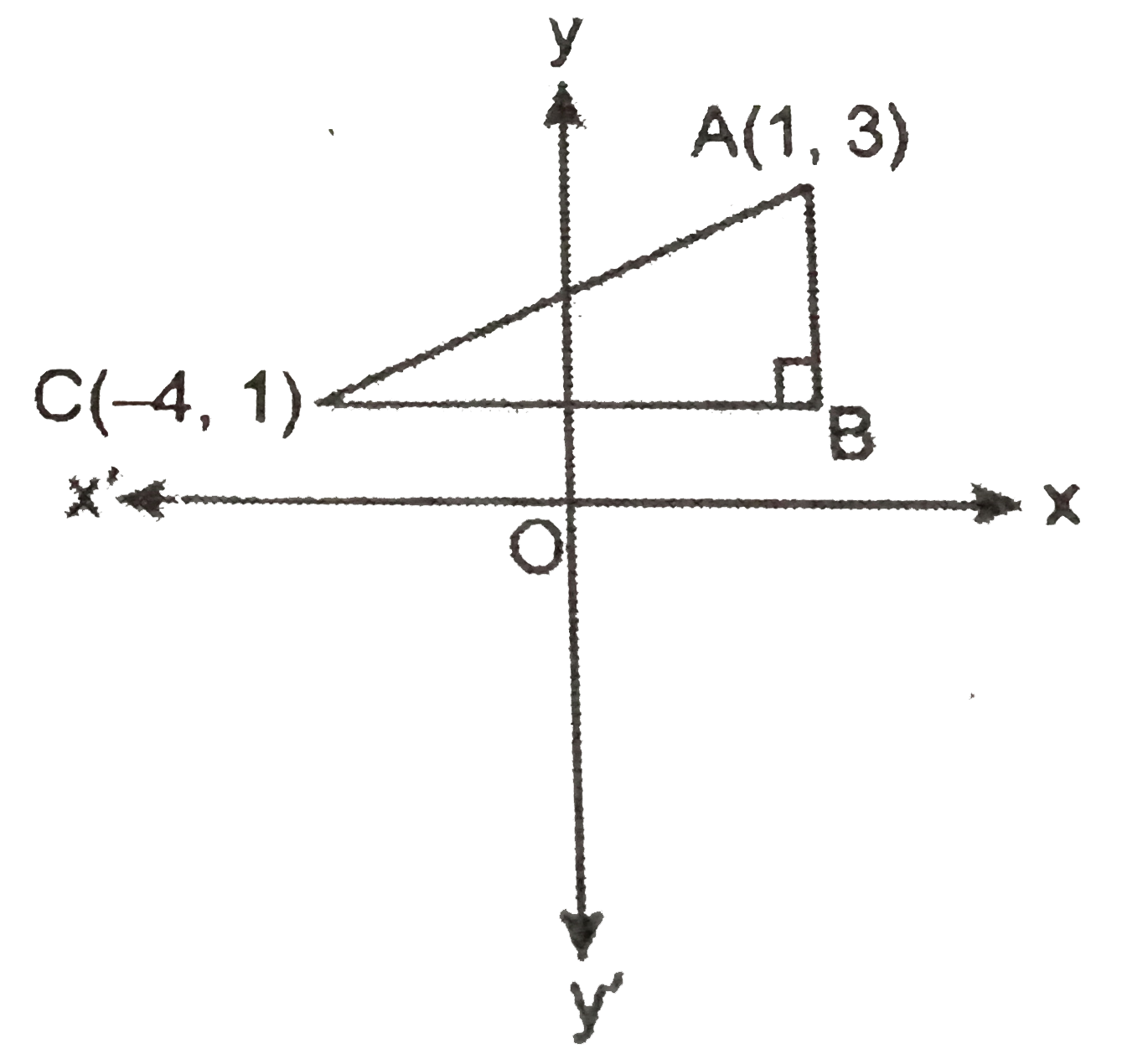
Let, in ΔABC
∠B=90∘
A≡(1,3)
and C≡(−4,1)
Equation of a line BC passing through C and parallel to x-axis is,
y=1
Similarly equation of a line AB passing through A and parallel to y-axis is
x=1
Similar Questions
The hypotenuse of a right angled triangle has its ends at the points (1,3) and (−4,1). Find an equation of the legs (perpendicular sides) of the triangle.
View SolutionThe hypotenuse of a right angled triangle has its ends at the points (1,3)and(−4,1). Find an equation of the legs (perpendicular sides) of the triangle.
View SolutionThe hypotenuse of a right angled triangle has its ends at the points (1, 3) and ( 4, 1) . Find the equation of the legs (perpendicular sides) of the triangle.
View SolutionThe hypotenuse of a right angled triangle has its ends at the points (1,3)and(−4,1). Find an equation of the legs (perpendicular sides) of the triangle.
View SolutionThe hypotenuse of a right angled triangle has its ends at the points (1, 3) and (- 4, 1). Find an equation of the legs (perpendicular sides) of the triangle.
View SolutionThe hypotenuse of a right angled triangle has its ends at the points (1,3) and (-4,1). Find the equation of the legs (perpendicular sides) of the triangle.
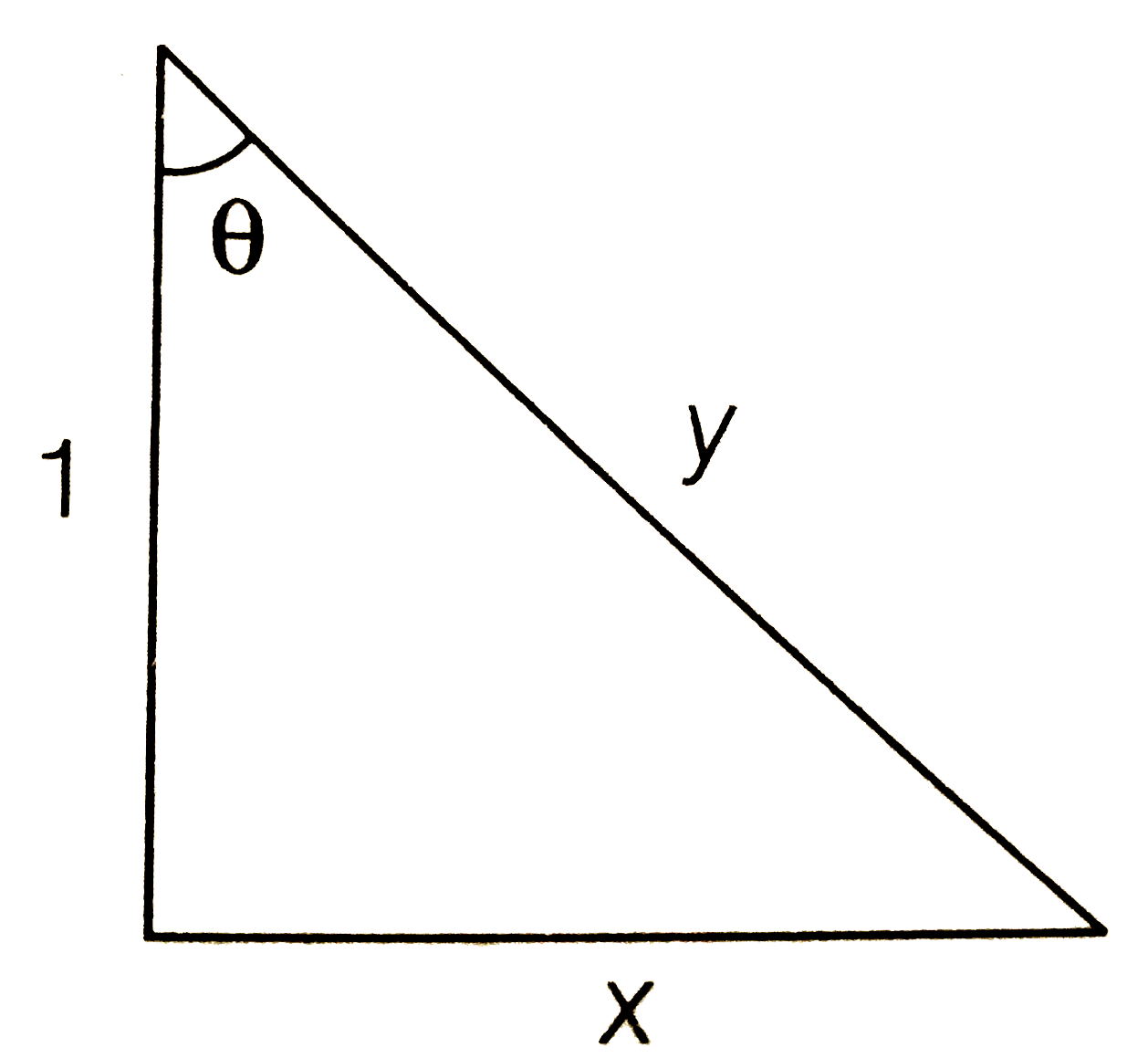
View SolutionA right angled triangle has legs 1 and x. The hypotenuse is y and angle opposite to the side x is θ. Shown as

View SolutionThe hypotenuse of a right angled triangle has its ends at the points (1, 3) and ( −4, 1) . Find the equation of the legs (perpendicular sides) of the triangle.
View Solution

