Derive the expression for magnetic field at a point on the axis of a circular current loop. Solution in Kannada
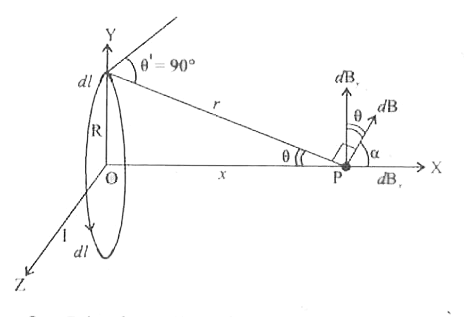
Let R be the radius of a current loop, carrying current I. Let R be a point on the axis of a conductor. Let dB be magnetic field at P, due to a current element .idl.
From the figure, θ+a=90∘, so that α=90∘–0 and cosα=cos(90∘–0)
sinθ=R2(R2+x2)12...(1)
Let dBx be the horizontal component of dB.
Applying Biot-Savart.s law ,
We write
d→B=(μ04π)I(d→l×→r)r3
i.e., dB=(μ04π)Irdlr3sinθ.
where θ.=90∘
i.e., dB=(μ04π)Irdlr3=(μ04π)Idlr2 ...(2)
Component of dB along the horizontal is
dBx=dBcosα
or dBx=dBsinθ
=(μ04π)Idlr2sinθ
By using (1) we write
dBx=(μ04π)Idlr2Rr=(μ04π)IdlR(R2+x2)32...(3)
or integrating
Bx=∫dBx=∫(μ04π)IR(R2+x2)32dl
i.e., Bx=(μ04π)IR(R2+x2)32dl
i.e., Bx=(μ04π)IR(R2+x2)32(2πR)
where ∫dl=2πR
or Bx=(μ04π)⎛⎜⎝2πIR2(R2+x2)32⎞⎟⎠ tesla
and →B=Bxˆi=(μ04π)⎛⎜⎝2πIR2(R2+x2)32⎞⎟⎠ˆi,
dBy=0
For a circular loop , and at the centre , x=0
→B=(μ04π)(2πIR)ˆi
For a circular conductor containing n turns ,
Bxˆi=(μ04π)2πnIR2(R2+x2)32ˆi
and at the centre ,
B0ˆi=(μ04π)(2πnIR)ˆi
Similar Questions
Derive the expression for magnetic field at a point on the axis of a circular current loop.
View SolutionDerive the expression for magnetic field at a point on the axis of a circular current loop.
View SolutionDerive the expression for magnetic field at a point on the axis of a circular current loop.
View SolutionDerive an expresion for the magnetic field at any point on the axis of a circular current loop.
View SolutionUsing Biot Savart’s law derive an expression for the magnetic field due to a circular current carrying loop at any point on its axis.
View SolutionDerive the expression for magnetic field at a point on the axis of a circular current loop.
View SolutionGive an expression for magnetic field on the axis of a circular current loop. (Expression only).
View SolutionBiot - Savart's law relates current with the magnetic field produced by it. Using the law derive an expression for intensity of magnetic field at a point at distance x from the center and on the axis of a circular current loop
View Solution
