Obtain the expression for fringe width in the case of interference of light waves.Solution in Kannada
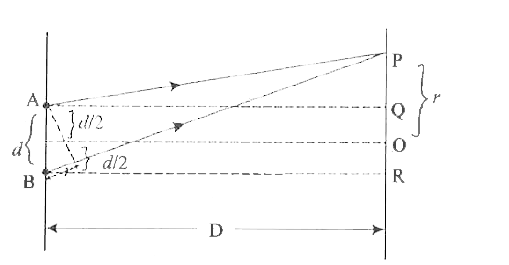
A and B represented two coherent sources separated by a distance d.
Let a screen be placed at a distance D from the sources. The point θ on the screen is equidistant from A and B .
It is given
BP-AP=δ
eqn.(1)-(2)
Then δ=BP2−AP2
In the
△le BRP, BP2=BR2+PR2=D2+(PO+OR)2
BP2=D2+(x+d/2)2...(1)
In the △le APQ,
AP2=AQ2+QP2=D2+(OP−OQ)2
AP2=D2+(x−d/2)2 ....(2)
BP2−AP2=D2+(x+d/2)2−D2+(x−d/2)2
=[D2+x2+d24+2xd/2]−[D2+x2+d24−2xd/2]
=cancelD^2+cancelx^2+cancel(d^2/4)+xd -cancelD^2-x^2-cancel(d^2/4)+xd
=xd+xd=2xd
(BP2−AP2)=2xd
(BP-AP)(BP+AP)=2xd
BP−AP=2xd(BP+AP)
BP-AP=(cancel2xd)/(cancel2D) P is very close to D
Path Difference Δ=xdD Δ is not shown in drawing .
For constructive interference δ=nλ
nλ=xdD⇒x=Dnλd
x1=Dλd⇒x2=2Dλd
The distance between the centers of any two consecutive bright fringes is called the fringe width.
β=x2−x1=2Dλd−Dλd
β=Dλd
Similar Questions
Answer the following: With a diagram showing the Young's arrangement for producing 'a sustained interference pattern, obtain the expression for the width of the interference fringes obtained in this pattern.
View SolutionObtain the expression for fringe width in the case of interference of light waves.
View SolutionObtain the expression for fringe width in the case of interference of light waves.
View SolutionDerive an expression for fringe width in Young's double slit interference of light.
View SolutionDescribe Young.s double slit experiment for the interference of light. Obtain the expression for fringe width.
View SolutionIn interference with two coherent beams of light , the fringe width is
View SolutionDefine coherent sources of light, fringe width and interference of light. Show that the width of dark fringe is equal to the width of bright fringe in Young's double slit experiment.
View SolutionObtain the expression for the fringe width interference fringes in Young's Double slit experiment .
View Solution

