State and prove parallel axis theoremSolution in Tamil
Video Solution
Text Solution
Parallel axis theorem. Parallel axis theorem states that the moment of inertia of a body about any axis is equal to the sum of its moment of inertia about a parallel axis through its centre of mass and the product of the mass of the body and the square of the perpendicular distance betwen the two axes.
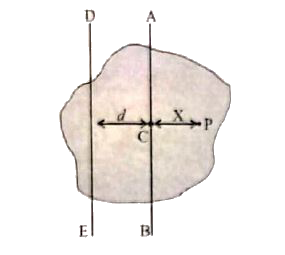
If IC is the moment of inertia of the body of mass M about an axis passing through the centre of mass, then the moment of inertia I about a parallel axis at a distance d from it is given by:
I=IC+Md2
Let us consider a rigid body as shown in the figure. Its moment of inertia about an axis AB passing thorugh the centre of mass is IC. Let DE be another axis parallel to AB at a perpendicular distance d from AB. The moment fo inertia of the body about DE is I. Let us attempt to get an express for moment of inertia of the body in tems of IC. For this, let us consider a point mass m on the body at position x from its centre of mass.
The moment of inertia of the point mass baout the axis DE is m(x+d)2.
The summation of the above expression given by the moment of inertia I of the whole body about DE is
I=Σm(x+d)2
I=Σm(x2+d2+2xd)
1=Σ(mx2+md2+2dmx)
1=Σx2+Σd2+2dΣmx)
Here Σmx2 is the moment of inertia of the body about the centre of mass.
∴IC=Σmx2
The term Σm=0, because x can take positive and negative values with respect to the axis AB.
Thus I=IC+Σmd2=IC=(Σm)d2
Here Σm is the entire mass M of the object (Σm=M)
I=IC+md2
Hence, the parallel axis theorem is proved.
|
Similar Questions
State and prove parallel axis theorem
View SolutionState and prove parallel axis theorem
View SolutionState and prove perpendicular axis theorem.
View SolutionState and prove parallel axis theorem
View SolutionState and prove parallel axis theorem
View SolutionState and prove theorem of parallel axis.
View SolutionState and prove theorem of parallel axes.
View Solution
