Factorise : (2x2+5x)(2x2+5x−19)+84
Text Solution
Let 2x2+5x=a
∴ Given expression reduces to
a(a−19)+84=a2−19a+84
Here, a=1, b=-19, c=84
∴ac=1×84=84
Now, we take two factors of 84 whose sum is -19. Such factors are -7 and -12.
∴a2−19a+84=a2−7a−12a+84
=a(a−7)−12(a−7)=a(a−7)(a−12)
=(2x2+5x−7)(2x2+5x−12)
Similarly, these can also be factorised further.
2x2+5x−7=2x2+7x−2x−7
=(2x+7)-1(2x+7)
=(2x+7)(x-1)
and 2x2+5x−12=2x2+8x−3x−12
=2x(x+4)-3(x+4)=(x+4)(2x-3)
∴ From (1), (2) and (3), we get
(2x2+5x)(2x2+5x−19)+84
=a2−19a+84 (wherea=2x2+5x)
=(2x+7)(x-1)(x+4)(2x-3)
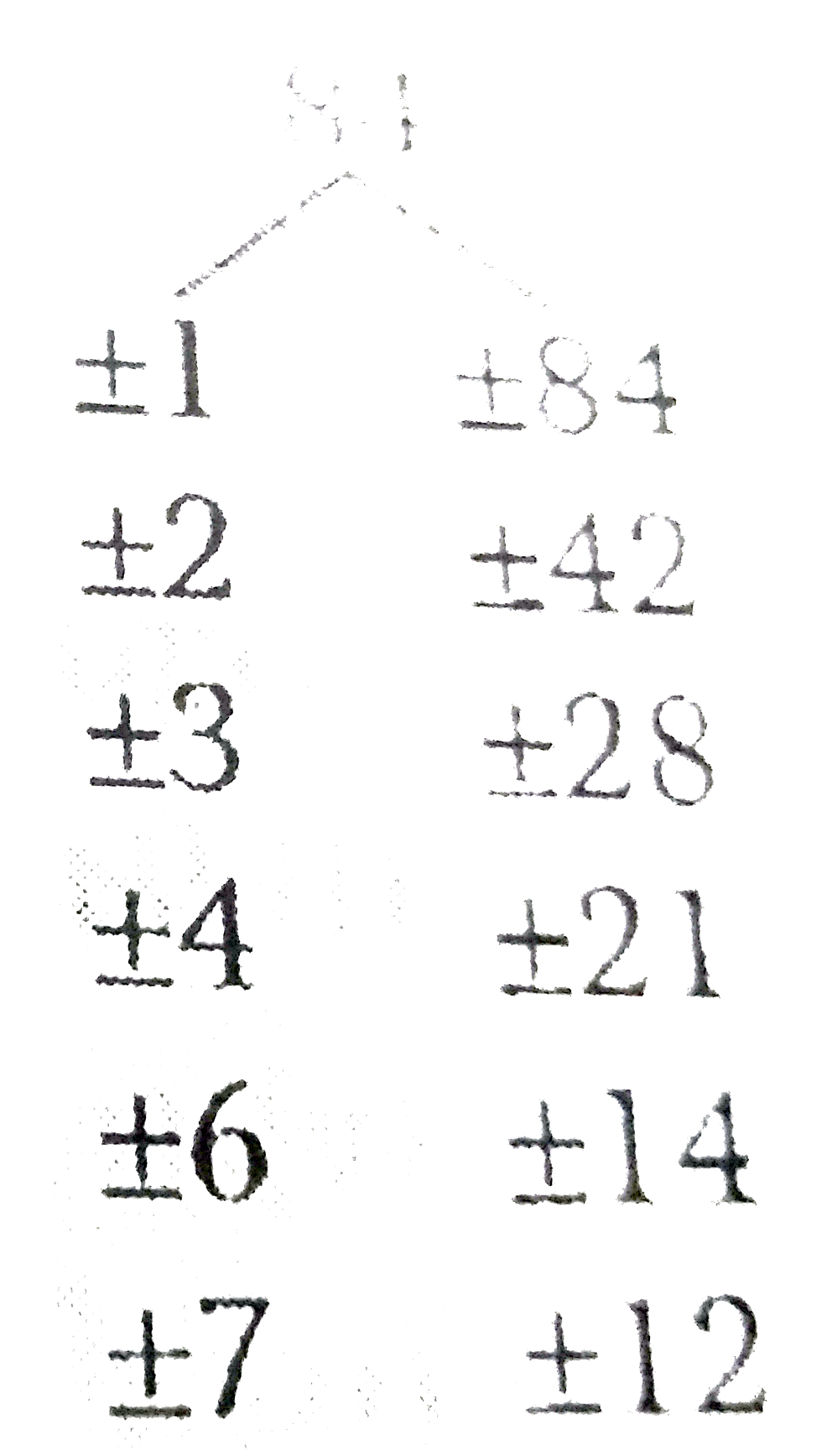
|
Similar Questions
Knowledge Check
Factorise : x4+5x3+5x2−5x−6
A(x2−1)(x2+6)B(x−1)(x+2)3C(x2−1)(x+3)(x+2)D(x−1)(x+2)(x2+3)Factorise:
x2−5x−24A(x−8)(x−3)B(x−8)(x+3)C(x+8)(x+3)Dnone of these
