If h,c,V are respectively the height, the curved surface and the volume of a cone, prove that 3πVh3−C2h2+9V2=0.
We know that : C=πrl,V=13πr2h,l2=h2+r2
L.H.S.=3πVh3−C2h2+9V2
=3π(13πr2h)h3−(πrl)2h2+9(13πr2h)2
π2r2h4−π2r2h2(h2+r2)+9×19π2r4h2 (∵l2=h2+r2)
=π2r2h4−π2r2h4−π2r4h2+π2r4h2
= 0 = R.H.S.
Topper's Solved these Questions
- SURFACE AREA AND VOLUMEBOOK - NAGEEN PRAKASHANCHAPTER - SURFACE AREA AND VOLUMEEXERCISE - Problems From NCERT/exemplar
24 Videos
- SURFACE AREA AND VOLUMEBOOK - NAGEEN PRAKASHANCHAPTER - SURFACE AREA AND VOLUMEEXERCISE - Exercise 13a
30 Videos
- STATISTICSBOOK - NAGEEN PRAKASHANCHAPTER - STATISTICSEXERCISE - Revision Exercise
10 Videos
- TRIANGLESBOOK - NAGEEN PRAKASHANCHAPTER - TRIANGLESEXERCISE - Revision Exercise (long Answer Type Question)
8 Videos
Similar Questions
The floor of a rectangular hall has a perimeter 250 m. If the cost of painting the four walls at the rate of Rs 10 per m2is Rs 15000, find the height of the hall.[Hint : Area of the four walls = Lateral surface area.]
View SolutionFind the volume and total surface area of a cuboid whose length = 3.5 m, breadth = 2.6 m and height = 0.9 m.
View SolutionIf the heights of 5 persons are 140 cm, 150cm, 152 cm and 161 cm respectively. Find the mean height.
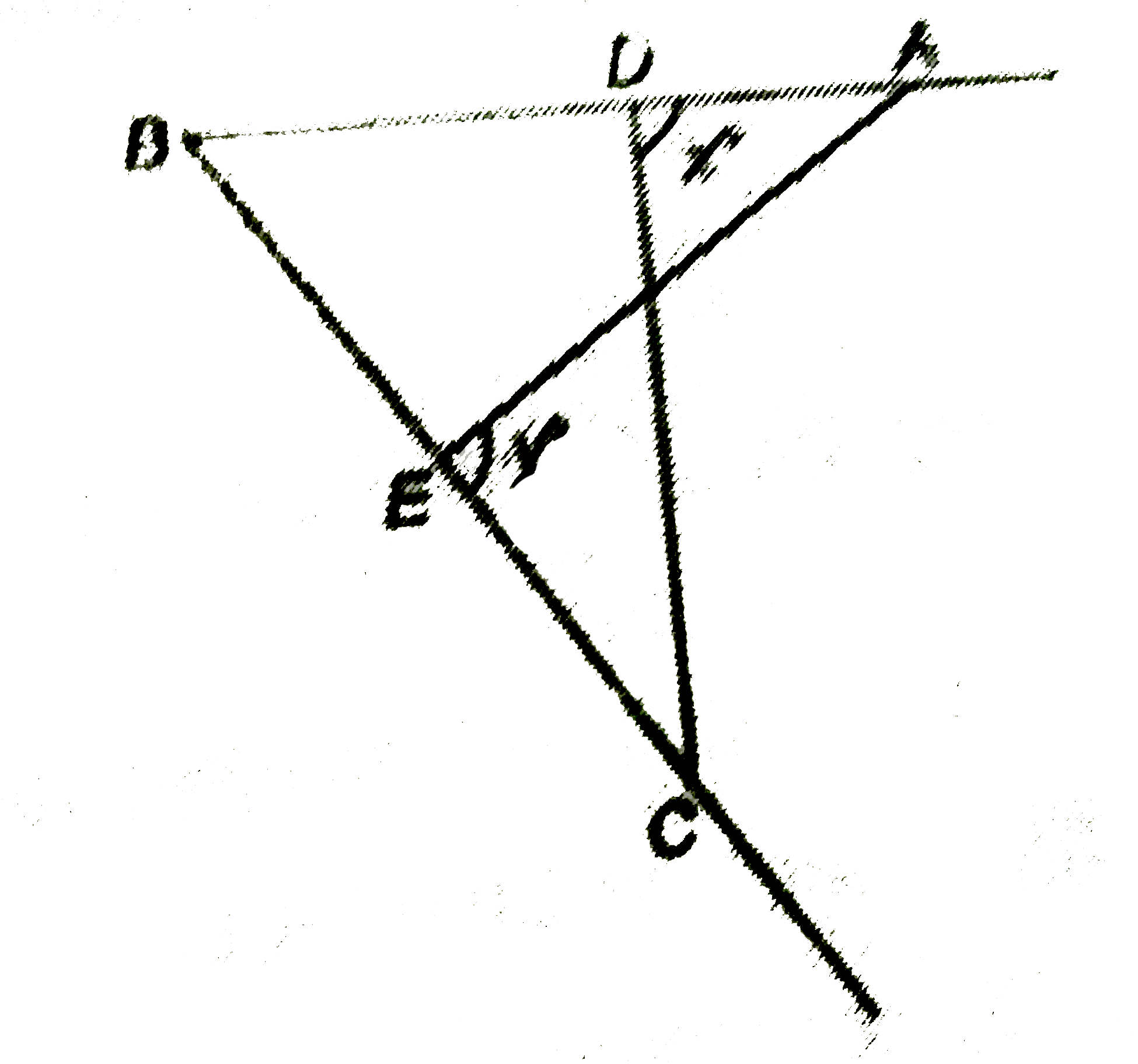
View SolutionIn the given figure, if x=y and AB=CB, then prove that AE=CD.
View SolutionIf h,c,V are respectively the height, the curved surface and the volume of a cone, prove that 3πVh3−C2h2+9V2=0.
View SolutionIf h,C,V respecitively are the height the curved surface area and volume of a cone prove that 3πVh3−C2h2+9V2=0
View Solutionयदि h, c, V क्रमशः एक शंकु की ऊँचाई, वक्र पृष्ठ तथा आयतन हों, तो सिद्ध करो कि 3πVh3−C2h2+9V2=0
View SolutionIf the height , curved surface area and volume of a right circular cone be h, c and v respectively , then that 3πvh3−c2h2+9v2=0.
View SolutionIf h,s V be the height , curved surface area and volume of a cone respectively , then (3πVh3+9V2−s2h2) is equal to :
View SolutionIf h,C,V represent height, curved surface area,
and volume of cone, prove that
3πVh3−C2h2+9V2=0.
View SolutionIf h,c,V are respectively the height, the curved surface and the volume of a cone, prove that 3πVh3−C2h2+9V2=0.
View SolutionIf h,c,V are respectively the height, the curved surface and the volume of a cone, prove that 3πVh3−C2h2+9V2=0.
View SolutionIf h, S and V denote respectively the height, curved surface area and volume of a right circular cone, then 3πVh3− S2h2+9V2 is equal to (a) 8 (b)0(c)4π(d)32π2
View Solutionयदि h, c और v क्रमश: एक शंकु की ऊँचाई, वक्रपृष्ठ और शंकु का आयतन हैं, तो 3πvh3−c2h2+9v2 का मान है
View SolutionIf h,s V be the height , curved surface area and volume of a cone respectively , then (3πVh3+9V2−s2h2) is equal to :
View SolutionIf h,c,V are respectively the height, the curved surface and the volume of a cone, prove that 3πVh3−C2h2+9V2=0.
View Solution
