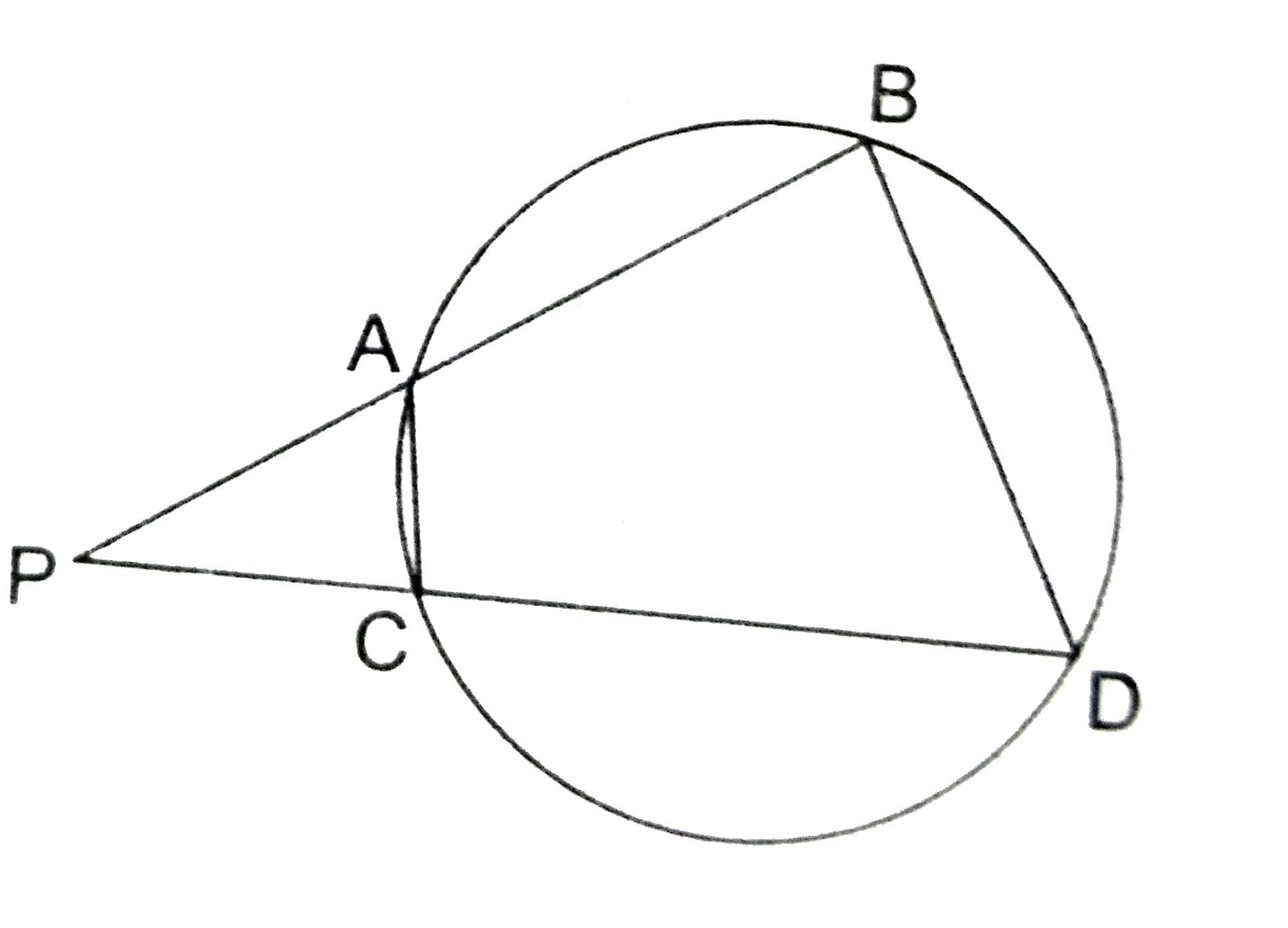
In Figure two chords AB and CD of a circle intersect each other at the point P (when produced) outside the circle. Prove that
(i) ΔPAC~ΔPDB
(ii) PA.PB=PC.PD

Video Solution
Text Solution
(i) In △PAC and △PDB,
∠BAC=180∘−∠PAC (linear pairs)
∠PDB=∠CDB=180−∠BAC
=180∘−(180∘−∠PAC)=∠PAC
∠PAC=∠PDB ... (1)
∠APC=∠BPD [Common] ... (2)
We know that in a cyclic quadrilateral, the exterior angle is equal to the interior opposite angle.
Therefore, for cyclic quadrilateral ABCD.
consider ABCD , ΔPAC and ΔPBD.
∠PCA=∠PBD .... (3)
∴ By AAA-criterion of similarity,
△PAC∼△DPB (proved)
(ii) △PAC∼△DPB
So, the corresponding sides of the similar triangles are proportional
PAPD=PCPD
⇒PA.PB=PC.PD
(proved)
|
Topper's Solved these Questions
- TRIANGLESBook:NCERTChapter:TRIANGLESExercise:EXERCISE 6.3
Explore 16 Videos
- TRIANGLESBook:NCERTChapter:TRIANGLESExercise:SOLVED EXAMPLES
Explore 14 Videos
- TRIANGLESBook:NCERTChapter:TRIANGLESExercise:Exercise 6.2
Explore 10 Videos
- SURFACE AREAS AND VOLUMESBook:NCERTChapter:SURFACE AREAS AND VOLUMESExercise:EXERCISE 13.2
Explore 8 Videos
Similar Questions
Knowledge Check
Two chords AB and CD of a circle intersects each other at P. which of the following is correct?
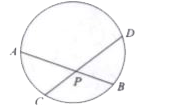 AAP×PB=CP×PDBAP+PB=CP×PDCAP−PB=CP−PDDAP×CP=BP×PD
AAP×PB=CP×PDBAP+PB=CP×PDCAP−PB=CP−PDDAP×CP=BP×PDTwo chords AB and CD of a circle with centre O intersect at point P within the circle. ∠AOC+∠BOD=?
A∠APCB2∠APCC32∠APCDNone of theseVinod have 20 rupees. He bought 1, 2, 5 rupee stamps. They are different in numbers by the reason of no change, the shop keeper gives 3 one rupee stamps. So how many stamps Vinod have ?
AA) 10BB) 18CC) 12DD) 15
In the figure, two chords AB and CD intersect each other at the point P.
Prove that : ΔAPC~ΔDPB

View SolutionIn the figure, two equal chords AB and CD of a circle with centre O, intersect each other at E, Prove that AD=CB
View SolutionIn the adjoining figure. If two equal chords AB and CD of a circle intersect each other at E. then prove that chords AC and DB are equal.

View SolutionIn a cricle, two chords AB and CD intersect at a point P inside the circle. Prove that
(a)ΔPAC~ΔPDB (b)PA⋅PB=PC⋅PD.
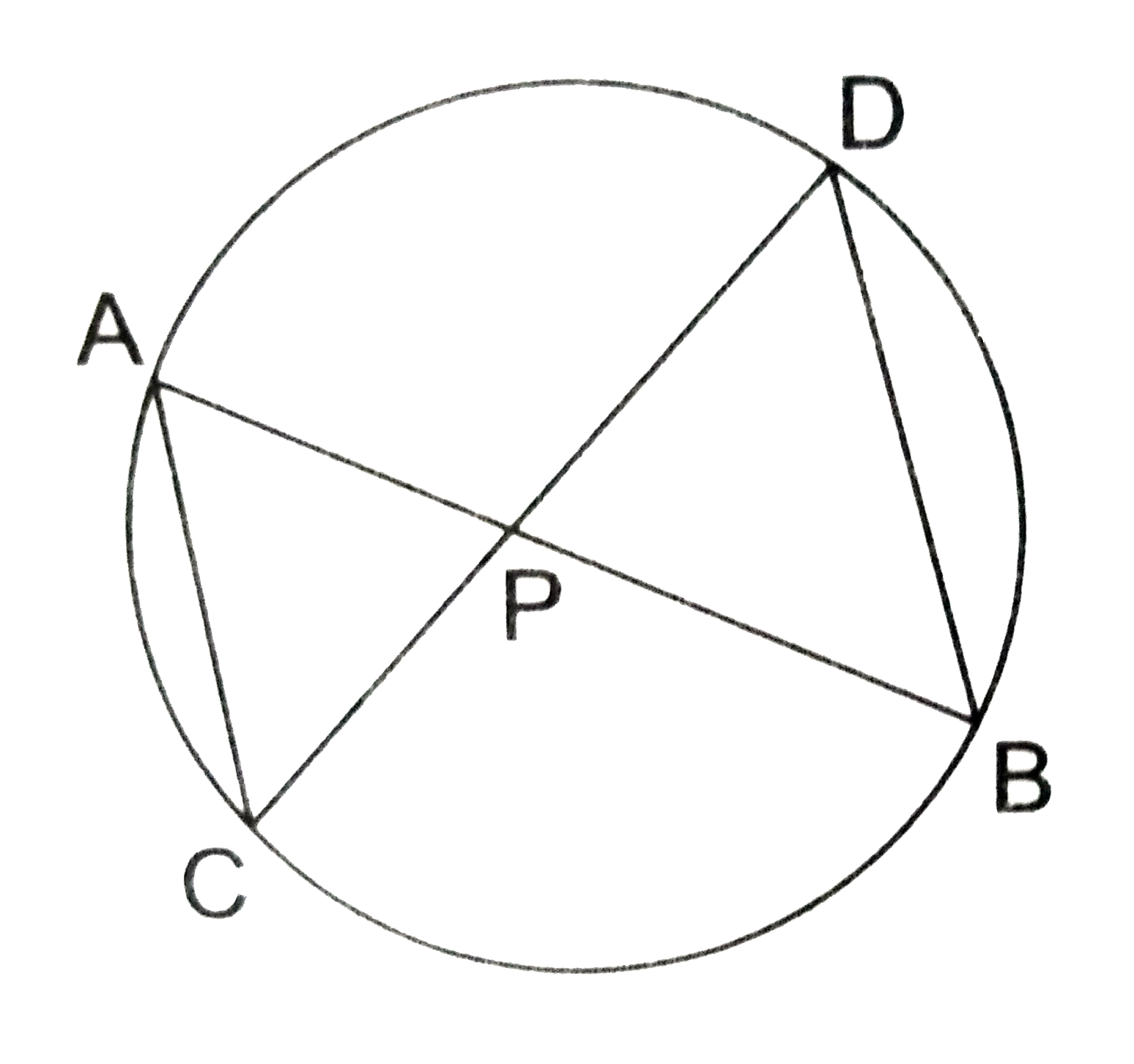
View SolutionIn Figure, two chords AB and CD intersect each other at the point P. Prove that:
(i) ΔAPC~ΔDPB
(ii) AP⋅PB=CP⋅DP

View Solution