If f(x)=⎧⎪⎨⎪⎩mx2+nx<0nx+m0<x≤1nx3+mx>1
For what integers m and n does both limx→0f(x) and limx→1f(x) exist?
Video Solution
Text Solution
at x=0
LHL=limx→0−f(x)
=limh→0f(0−h)
=limh→0m(0−h)2+n=n
RHL=limx→0+f(x)
=limh→0f(0+h)
=limh→0n(0+h)+m=m
∵limx→0f(x) exists.
Let 0−h=x
⇒0−h→0
⇒h→0
Let 0+h=x
⇒0+h→0
⇒h→0
|
Similar Questions
Knowledge Check
If f(x)=⎧⎪⎨⎪⎩mx2+x+n,x<0nx+m,0≤x≤12nx3+x2−2x+m,x>1
and limx→0f(x) and limx→1 f(x) exist thenAm=2,n=1Bm=0,n=1Cm=1,n=2Dm=1,n=1limx→0+(xnlnx),n>0
Adoes not existBexists and is zeroCexists and is 1Dexists and is e−1
If f(x)=⎧⎪⎨⎪⎩mx2+n,x<0nx+m,0≤x≤1nx3+m,x>1. For what integers m and n does limx→0f(x) and limx→1f(x) exist ?
View SolutionEvaluate limx→0f(x), where
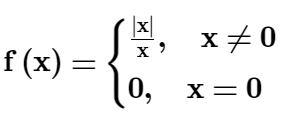
View SolutionIf f(x)=⎧⎪⎨⎪⎩|x|+1x<00x=0|x|−1x>0
for what value (s) of a does limx→af(x) exists?
View Solutionlimx→03√1+x−1x
View Solutionlimx→02x√1+x−1
View SolutionProve that limx→0(1+x)n−1x=n.
View Solution
