Diagonals of a trapezium ABCD with AB || DC intersect each other at the point O. If AB = 2 CD, find the ratio of the areas of triangles AOB and COD.
To solve the problem of finding the ratio of the areas of triangles AOB and COD in trapezium ABCD, where AB is parallel to CD and AB = 2CD, we can follow these steps:
1. Identify the Given Information:
- We have a trapezium ABCD with AB || CD.
- It is given that AB = 2CD.
2. Establish the Similarity of Triangles:
- Since AB is parallel to CD, we can use the properties of parallel lines and angles.
- The angles formed by the diagonals intersecting at point O will be:
- Angle AOB = Angle COD (vertically opposite angles)
- Angle OAB = Angle OCD (alternate interior angles)
- Angle OBA = Angle ODC (alternate interior angles)
- Therefore, triangles AOB and COD are similar by the AAA (Angle-Angle-Angle) criterion.
3. Use the Ratio of Corresponding Sides:
- The ratio of the areas of two similar triangles is equal to the square of the ratio of their corresponding sides.
- Let the length of CD be x. Then, AB = 2x.
- The ratio of the lengths of the sides is:
ABCD=2xx=2
4. Calculate the Ratio of the Areas:
- Since the areas of triangles AOB and COD are in the ratio of the square of the sides:
Areaof△AOBAreaof△COD=(ABCD)2=22=4
- Thus, the ratio of the areas of triangles AOB and COD is:
Areaof△AOBAreaof△COD=4:1
Final Answer:
The ratio of the areas of triangles AOB and COD is 4:1.
- We have a trapezium ABCD with AB || CD.
- It is given that AB = 2CD.
- Since AB is parallel to CD, we can use the properties of parallel lines and angles.
- The angles formed by the diagonals intersecting at point O will be:
- Angle AOB = Angle COD (vertically opposite angles)
- Angle OAB = Angle OCD (alternate interior angles)
- Angle OBA = Angle ODC (alternate interior angles)
- Therefore, triangles AOB and COD are similar by the AAA (Angle-Angle-Angle) criterion.
- The ratio of the areas of two similar triangles is equal to the square of the ratio of their corresponding sides.
- Let the length of CD be x. Then, AB = 2x.
- The ratio of the lengths of the sides is:
ABCD=2xx=2
- Since the areas of triangles AOB and COD are in the ratio of the square of the sides:
Areaof△AOBAreaof△COD=(ABCD)2=22=4
- Thus, the ratio of the areas of triangles AOB and COD is:
Areaof△AOBAreaof△COD=4:1
The ratio of the areas of triangles AOB and COD is 4:1.
Similar Questions
Diagonals of a trapezium ABCD with AB || DC, intersect each other at the point ‘O’. If AB = 2CD, find the ratio of areas of triangles AOB and COD.
View SolutionDigonals of a trapezium ABCD with AB∣∣DC intersect each other at the point O. If AB= 2 CD, find the ratio of the areas of triangles AOB and COD.
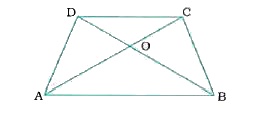
View SolutionDiagonals of a trapezium ABCD with AB || DC intersect each other at the point O. If AB = 2 CD, find the ratio of the areas of triangles AOB and COD.
View SolutionThe diagonals of a trapezium ABCD with AB||DC intersect each other at point O. If AB = 2CD, find the ratio of the areas of triangle AOB and COD.
View SolutionDigonals of a trapezium ABCD with AB∣∣DC intersect each other at the point O. If AB= 2 CD, find the ratio of the areas of triangles AOB and COD.

View Solutionएक समलंब चतुर्भुज □ABCD में, AB ∣∣ CD और AB = 2 CD हैं। AC तथा DB का प्रतिच्छेदन बिंदु O हैं , तो ΔAOB तथा ΔCOD के क्षेत्रफलों का अनुपात ज्ञात कीजिए।
View Solutionਇਕ ਸਮਲੰਬ ਚਤੁਰਭੁਜ ABCD ਜਿਸ ਵਿੱਚ AB II DC ਹੈ, ਦੇ ਵਿਕਰਣ ਆਪਸ ਵਿਚ O ਬਿੰਦੂ ਉੱਤੇ ਕੱਟਦੇ ਹਨ।ਜੇਕਰ AB=2 CD ਹੋਵੇ ਤਾਂ ਤ੍ਰਿਭੁਜਾਂ AOB ਅਤੇ COD ਦੇ ਖੇਤਰਫਲਾਂ ਦਾ ਅਨੁਪਾਤ ਪਤਾ ਕਰੋ।
View SolutionDiagonals of a trapezium ABCD withAB∣∣DC intersect each other at the point O.If AB=2 CD,find the ratio of the areas of triangle AOB and COD.
View Solution
