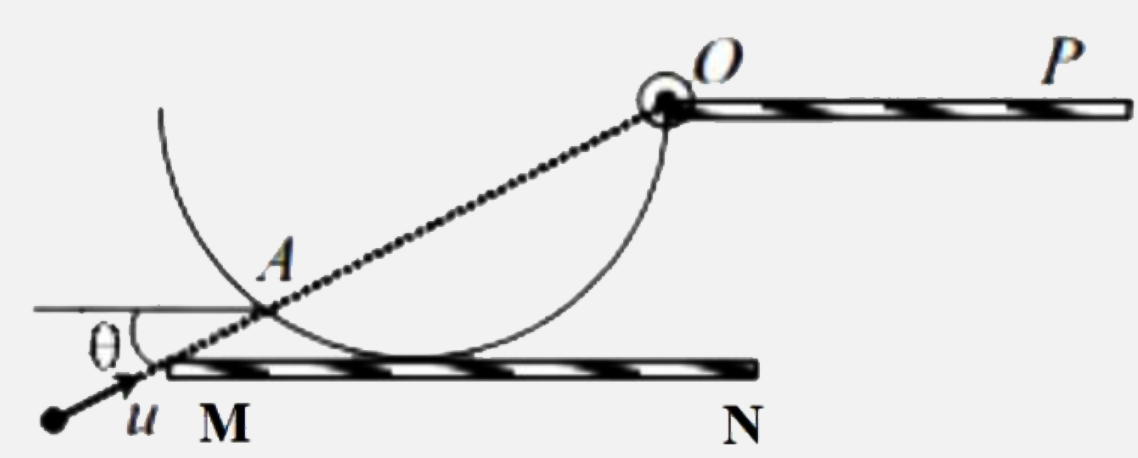
The diagram shows a hemispherical shell of mass m and radius R is hinged at point of placed on a horizontal surface. A ball of mass strikes the shell at point A ( as shown in the figure ) moving with velocity u inclined at an angle θ=tan−1(12) and then it stops . For the given shell to reach horizontal surface OP what minimum speed u is required ?
2√gR3
√2gR3
gR√5
Not possible
The correct Answer is:D
Step by step video & image solution for The diagram shows a hemispherical shell of mass m and radius R is hinged at point of placed on a horizontal surface. A ball of mass strikes the shell at point A ( as shown in the figure ) moving with velocity u inclined at an angle theta = tan^(-1) (1/2) and then it stops . For the given shell to reach horizontal surface OP what minimum speed u is required ? by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
Time taken by the sunlight to pass thought a slab of 4 cm and reflective index 1.5 is ………….s.
View SolutionThe potential of an atom is given by V=V0loge(r/r0) where r0 is a constant and r is the radius of the orbit Assumming Bohr's model to be applicable, which variation of rn with n is possible (n being proncipal quantum number)?
View SolutionThe figure shows a spherical shell of mass M. The point a is not at the centre but away from the centre of the shell. If a particle of mass m is placed at A, then

View SolutionA ball of mass m and radius r rolls inside a fixed hemispherical shell of radius R . It is released from rest from point A as shown in figure. The angular velocity of centre of the ball in position B about the centre of the shell is. .
View SolutionA cannon of mass 5m (including a shell of mass m) is at rest on a smooth horizontal ground, fires the shell with its barrel at an angle θ with the horizontal at a velocity u relative to cannon. Find the horizontal distance of the point where shell strikes the ground from the initial position of the cannon :-
View SolutionA particel of mass M is placed at the centre of a inform spherical shell of mass 2M and radius R. The gravitational potential on the surface of the shell is
View SolutionA body of mass m is placed at the centre of the spherical shell of radius R and mass M. The gravitation potential on the surface of the shell is
View SolutionA particle of mass M is placed at the centre of a uniform spherical shell of mass 2M and radius R. The gravitational potential on the surface of the shell is:
View SolutionA particle of mass M is placed at the centre of a uniform spherical shell of mass 2M and radius R. The gravitational potential on the surface of the shell is
View SolutionA particle of mass M is placed at the centre of a uniform spherical shell of mass 2M and radius R. The gravitational potential on the surface of the shell is
View SolutionA particle of mass M is placed at the centre of a uniform spherical shell of mass 2M and radius R. The gravitational potential on the surface of the shell is
View SolutionA particle of mass M is placed at the centre of a uniform spherical shell of mass 2M and radius R. The gravitational potential on the surface of the shell is
View SolutionThe figure shows a spherical shell of mass M . The point A is not at the centre but away from the centre of the shell. If a particle of mass m is placed at A , then
View SolutionA ball of mass m and radius r rolls inside a hemispherical shell of radius R . It is released from rest from point A as shown in figure. The angular velocity of centre of the ball in position B about the centre of the shell is. .
View SolutionA body of mass m is placed at the centre of the spherical shell of radius R and mass M. The gravitation potential on the surface of the shell is
View SolutionThe diagram shows a hemispherical shell of mass m and radius R is hinged at point of placed on a horizontal surface. A ball of mass strikes the shell at point A ( as shown in the figure ) moving with velocity u inclined at an angle theta = tan^(-1) (1/2) and then it stops . For the given shell to reach horizontal surface OP what minimum speed u is required ?
View Solution

