The place faces of two identical plano-convex lenses, each with focal length f are pressed against each other using an optical glue to from a usual convex lens .The distance from the optical centre at which an object must be placed to obtain the image same as the size of the object is
f4
f2
f
2f
The correct Answer is:C
To solve the problem, we need to determine the distance from the optical center at which an object must be placed to obtain an image that is the same size as the object when using two identical plano-convex lenses glued together.
1. Understanding the System:
- We have two identical plano-convex lenses, each with a focal length f.
- When these lenses are pressed together, they form a new lens system.
2. Finding the Focal Length of the Combined Lens:
- The formula for the focal length F of two lenses in contact is given by:
1F=1f1+1f2
- Since both lenses have the same focal length f:
1F=1f+1f=2f
- Therefore, the focal length F of the combined lens is:
F=f2
3. Using the Lens Formula:
- The lens formula relates the object distance u, image distance v, and focal length F:
1F=1v−1u
- Rearranging gives:
1u=1v−1F
4. Condition for Same Size Image:
- For the image to be the same size as the object, the magnification m must be 1:
m=h′h=vu=1⟹v=u
- Therefore, we can substitute v with u in the lens formula:
1F=1u−1u⟹1F=0
- This means we need to find the distance u where the image distance v equals u.
5. Substituting the Focal Length:
- From the earlier calculation, we have F=f2:
1u=1u−2f
- This leads to:
1u=2f
- Thus, solving for u:
u=f2
Final Answer:
The distance from the optical center at which the object must be placed to obtain an image the same size as the object is:
u=f
- We have two identical plano-convex lenses, each with a focal length f.
- When these lenses are pressed together, they form a new lens system.
- The formula for the focal length F of two lenses in contact is given by:
1F=1f1+1f2
- Since both lenses have the same focal length f:
1F=1f+1f=2f
- Therefore, the focal length F of the combined lens is:
F=f2
- The lens formula relates the object distance u, image distance v, and focal length F:
1F=1v−1u
- Rearranging gives:
1u=1v−1F
- For the image to be the same size as the object, the magnification m must be 1:
m=h′h=vu=1⟹v=u
- Therefore, we can substitute v with u in the lens formula:
1F=1u−1u⟹1F=0
- This means we need to find the distance u where the image distance v equals u.
- From the earlier calculation, we have F=f2:
1u=1u−2f
- This leads to:
1u=2f
- Thus, solving for u:
u=f2
The distance from the optical center at which the object must be placed to obtain an image the same size as the object is:
u=f
Similar Questions
Knowledge Check
The plane faces of two identical plano convex lenses, each with focal length f are pressed against each other using an optical glue to form a usual convex lens. The distance from the optical centre at which an object must be placed to obtain the image same as the size of object is
Af4Bf2CfD2fThe plane faces of two identical planoconvex lenses each having focal length of 40cm are pressed against each other to form a usual convex lens. The distance from this lens, at which an object must be placed to obtain a real, inverted image with magnification one is
A80cmB40cmC20cmD162cmThe plane faces fo two identical plano-convex lenses each having a focal length of 50 cm are placed against each other to form a usual biconvex lens. The distance from this lens combination at which an object must be placed to obtain a real, inverted image which has the same size as the object is
A50 cmB25 cmC100 cmD40 cm
Calculate two possible distances of an object from a convex lens of focal length 20 cm so as to obtain an image of double the size of the object.
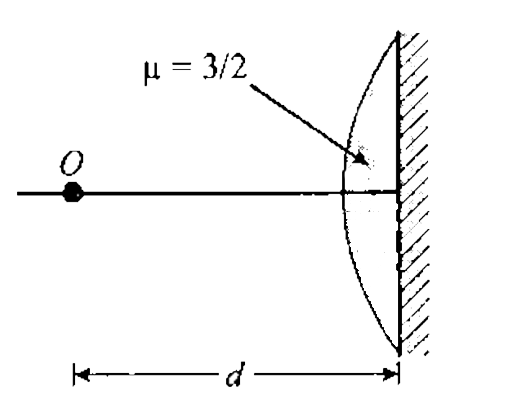
View SolutionA plano-convex lens of focal length 10 cm is silvered at its plane face. The distance d at which an object must be placed in order to get its image on itself is:
View SolutionAt what distance from a convex lens of focal length 30cm a object should be placed so that the size of image be14that of object?
View SolutionA plano-convex lens of focal length 30 cm has its plane surface silvered. An object is placed 40 cm from the lens on the convex side. The distance of the image from the lens is
View SolutionA convex lens of focal length 15 cm is placed in front of a plane mirror at a distance 25 cm from the mirror. Where on the optical axis and from the centre of the lens should a small object be placed such that the final image coincides with the object ?
View Solution

