A tank is filled with water of density 1gcm−3 and oil of density 0.9gcm−3 . The height of the water layer is 100 cm and of the oil layer is 400 cm. If g = 980 cms−2 , then the velocity of efflux from an opening in the bottom of the tank is
√920×980 cm s−1
√900×980 cm s−1
√1000×980 cm s−1
√92×980 cm s−1
The correct Answer is:A
To solve the problem, we need to find the velocity of efflux from an opening at the bottom of a tank filled with water and oil. We will use Torricelli's theorem, which states that the velocity of efflux (v) from an opening under the influence of gravity is given by:
v=√2gh
where g is the acceleration due to gravity and h is the effective height of the fluid column above the opening.
1. Identify the densities and heights:
- Density of water (ρw) = 1 g/cm³
- Density of oil (ρo) = 0.9 g/cm³
- Height of water (hw) = 100 cm
- Height of oil (ho) = 400 cm
- Acceleration due to gravity (g) = 980 cm/s²
2. Calculate the pressure at the bottom of the tank:
The pressure at the bottom of the tank is due to both the water and the oil layers. The pressure due to a fluid column is given by:
P=ρgh
Therefore, the total pressure at the bottom (Ptotal) is the sum of the pressures due to the water and the oil:
Ptotal=Pwater+Poil=ρwghw+ρogho
Substituting the values:
Ptotal=(1g/cm3)(980cm/s2)(100cm)+(0.9g/cm3)(980cm/s2)(400cm)
3. Calculate each pressure:
- Pressure due to water:
Pwater=1×980×100=98000dyne/cm2
- Pressure due to oil:
Poil=0.9×980×400=352800dyne/cm2
4. Total pressure at the bottom:
Ptotal=98000+352800=450800dyne/cm2
5. Calculate the effective height (h) for the velocity of efflux:
To find the effective height h that corresponds to the total pressure, we can use the formula for pressure again:
Ptotal=ρwgh
Rearranging gives:
h=Ptotalρwg=4508001×980=460cm
6. Calculate the velocity of efflux using Torricelli's theorem:
Now we can find the velocity of efflux:
v=√2gh=√2×980×460
Calculate:
v=√902800≈950.84cm/s
Final Answer:
The velocity of efflux from the opening in the bottom of the tank is approximately 950.84cm/s.
- Density of water (ρw) = 1 g/cm³
- Density of oil (ρo) = 0.9 g/cm³
- Height of water (hw) = 100 cm
- Height of oil (ho) = 400 cm
- Acceleration due to gravity (g) = 980 cm/s²
The pressure at the bottom of the tank is due to both the water and the oil layers. The pressure due to a fluid column is given by:
- Pressure due to water:
Pwater=1×980×100=98000dyne/cm2
- Pressure due to oil:
Poil=0.9×980×400=352800dyne/cm2
Ptotal=98000+352800=450800dyne/cm2
To find the effective height h that corresponds to the total pressure, we can use the formula for pressure again:
Now we can find the velocity of efflux:
The velocity of efflux from the opening in the bottom of the tank is approximately 950.84cm/s.
Similar Questions
Find the volume of 900 g of cooking oil whose density is 0.9g/cm3. Give the answer in litres.
View SolutionA oil droplet of density 0.97 g//cm^3 and radius 10^-4 cm is falling down through air, density & coefficient of viscosity of air is 0.0013 g//cm^3 and 181 xx 10^-6 CGS respectively. Calculate the terminal velocity of the water droplet, (g = 980 cm//s^2) .
View SolutionA tank is filled with water of density 103kg/m3 and oil of density 0.9×103kg/m3.The height of water layer is 1m and that of the oil layer is 4M. The velocity of efflux front an opening in the bottom of the tank is
View SolutionHeight of oil column =h3=20cm
Height of water column =h1+h2=50cm
Height of orifice from bottom =h1=20cm
Density of water =1g/cm3
Density of oil =0.75g/cm3
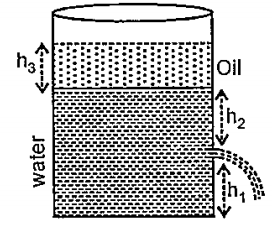
Orifice is very narrow compare to the cylinder. The velocity of efflux is
View SolutionDensity of water is 1.00g/cm3 and density of ethanol is 0.9g/cm3. If these two liquids were mixed to prepare a dilute solution then
View SolutionA metal tablet with a radius of 0.3 cm 0.94 g cm^(-3) The density falls into the oil layer. If it 0.5 cm s^(-1) Find the oil coefficient coefficient if moving at the final velocity of no. Metal density 7.8 g cm^(-3) Is.
View SolutionA spherical oil drop falls at a steady rate of 2 cm/s in still air. Find diameter of the drop . Take g =980 cm/s^2 . The coefficient of viscosity of air is 1.8 xx 10^(-4) Poise, Density of oil = 0.8 gm/ cm^3 , Density of air = 1 gm/ cm^3
View SolutionA tank 5 m high is half filled with water and then is filled to top with oil of density 0.85g/cm3 The pressure at the bottom of the tank, due to these liquids is
View Solution
