From a point P(3, 3) on the circle x2+y2=18 two chords PQ and PR each of he length 2 units are drawn on this circle. Then, the value of the length PM is equal to (where, M is the midpoint of the line segment joining Q and R)
13√2 units
12 units
√23 units
49 units
The correct Answer is:C
To solve the problem step by step, we will follow the geometric and algebraic approach to find the length of PM, where M is the midpoint of the line segment joining points Q and R on the circle.
Step 1: Verify Point P on the Circle
First, we need to confirm that the point P(3, 3) lies on the circle defined by the equation x2+y2=18.
32+32=9+9=18
Since this holds true, point P is indeed on the circle.
Hint: Always verify if the given point lies on the circle by substituting its coordinates into the circle's equation.
Step 2: Determine the Circle's Radius
The equation of the circle is x2+y2=18. The radius r can be calculated as:
r=√18=3√2
Hint: The radius of a circle can be found by taking the square root of the constant term in the circle's equation.
Step 3: Understand the Geometry
From point P, two chords PQ and PR are drawn, each of length 2 units. Let O be the center of the circle (0, 0). The distances from O to P, Q, and R are equal to the radius 3√2.
Hint: Visualize the problem by sketching the circle and marking the points P, Q, and R.
Step 4: Apply the Cosine Rule in Triangle OQP
In triangle OQP, we can apply the cosine rule to find the angle θ at point O:
OQ2=OP2+PQ2−2⋅OP⋅PQ⋅cos(θ)
Substituting the known values:
(3√2)2=(3√2)2+22−2⋅(3√2)⋅2⋅cos(θ)
This simplifies to:
18=18+4−12√2cos(θ)
Rearranging gives:
12√2cos(θ)=4⟹cos(θ)=13√2
Hint: The cosine rule relates the lengths of the sides of a triangle to the cosine of one of its angles.
Step 5: Find Length PM
In triangle QMP, we can use the cosine of angle θ to find PM:
cos(θ)=PMQP
Substituting the known values:
13√2=PM2
Solving for PM gives:
PM=23√2=√23
Hint: Use the relationship between the sides of the triangle and the cosine of the angle to find the desired length.
Final Answer
The length of PM is:
√23
First, we need to confirm that the point P(3, 3) lies on the circle defined by the equation x2+y2=18.
The equation of the circle is x2+y2=18. The radius r can be calculated as:
From point P, two chords PQ and PR are drawn, each of length 2 units. Let O be the center of the circle (0, 0). The distances from O to P, Q, and R are equal to the radius 3√2.
In triangle OQP, we can apply the cosine rule to find the angle θ at point O:
In triangle QMP, we can use the cosine of angle θ to find PM:
The length of PM is:
Topper's Solved these Questions
Similar Questions
Find the value of a, for which point P(a3,2) is the midpoint of the line segment joining the points Q(−5,4)andR(−1,0).
View SolutionPerpendiculars are drawn, respectively, from the points PandQ to the chords of contact of the points QandP with respect to a circle. Prove that the ratio of the lengths of perpendiculars is equal to the ratio of the distances of the points PandQ from the center of the circles.
View Solution
Knowledge Check
From a point P(3, 3) on the circle x2+y2=18 , two chords PQ and PR each of 2 units length are drawn on this circle. The value of cos (∠QPR) is equal to
A13√2B−89C√23D−49From a point A(1, 1) on the circle x2+y2−4x−4y+6=0 two equal chords AB and AC of length 2 units are drawn. The equation of chord BC, is
A4x+3y-12=0Bx+y=4C3x+4y=4Dx+y=6The two lines through (2,3) from which the circle x2+y2=25 intercepts chords of length 8 units have equations
A2x+3y=13,x+5y=17By=3,12x+5y=39Cx=2,9x−11y=51Dnone of these

A point P is 13 cm from the centre of the circle. The two tangent PQ and PR are drawn from the point P, The length of the tangent drawn from P to the circle is 12 cm.
Find the radius of the circle.
View SolutionTheorem of internal division of chords.
Suppose two chords of a circle intersect each other in the interior of the circle, then the product of the lengths of the two segments of one chord is equal to the product of the lengths of the two segments of the other chord.
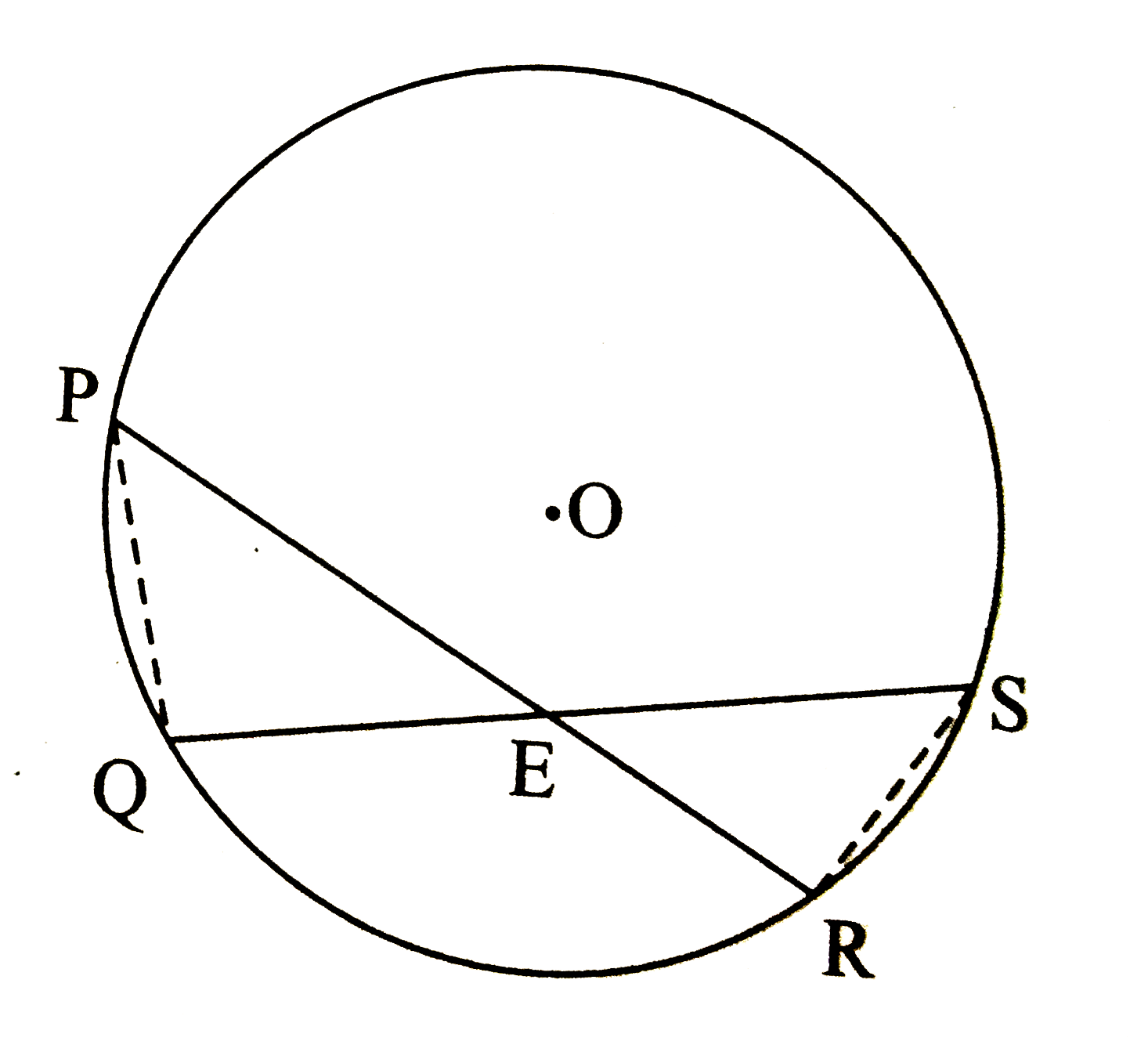
Given : (1) A circle with centre O .
(2) chords PR and QS intersect at point E inside the circle.
To prove : PE × ER = QE xx ES <br>Construction: Draw seg PQ and seg RS
View SolutionTwo tangents are drawn from the point P(−1,1) to the circle x2+y2−2x−6y+6=0. If these tangen tstouch the circle at points A and B, and if D is a point on the circle such that length of the segments AB and AD are equal, then the area of the triangle ABD is equal to
View SolutionA variable point P is on the circle x2+y2=1 on XY-plane. From point P perpendicular PN is drawn to the line L:x-2=y-2=-z, then minimum length PN drawn is
View SolutionTangents drawn from the point (4,4) to the circle
x2+y2−2x−2y−7=0 meets the circle at A andB then the length of chord AB is equal to
View Solution
