An L.C, R series circuit is connected to ac, source. At resonance, the applied voltage and the current flowing through the circuit will have a phase difference of
π/4
zero
pi
π/2
The correct Answer is:B
To solve the problem of finding the phase difference between the applied voltage and the current flowing through an LCR series circuit at resonance, we can follow these steps:
1. Understanding the Circuit:
- An LCR series circuit consists of an inductor (L), capacitor (C), and resistor (R) connected in series to an AC voltage source.
- At resonance, the inductive reactance (X_L) and capacitive reactance (X_C) are equal.
2. Condition at Resonance:
- At resonance, the condition is given by:
XL=XC
- This implies that the current through the inductor (I_L) and the current through the capacitor (I_C) are equal in magnitude but opposite in phase.
3. Current in the Circuit:
- The current through the resistor (I_R) is in phase with the applied voltage (V).
- Since I_L and I_C are equal and opposite, they effectively cancel each other out at resonance.
4. Net Current:
- The net current (I) in the circuit is the same as the current through the resistor (I_R) because the effects of I_L and I_C cancel each other out.
- Therefore, the net current is in phase with the applied voltage.
5. Phase Difference:
- Since the net current (I) is in phase with the applied voltage (V), the phase difference between the applied voltage and the current flowing through the circuit at resonance is:
Phase Difference=0∘
Conclusion:
At resonance in an LCR series circuit, the phase difference between the applied voltage and the current flowing through the circuit is 0 degrees.
- An LCR series circuit consists of an inductor (L), capacitor (C), and resistor (R) connected in series to an AC voltage source.
- At resonance, the inductive reactance (X_L) and capacitive reactance (X_C) are equal.
- At resonance, the condition is given by:
XL=XC
- This implies that the current through the inductor (I_L) and the current through the capacitor (I_C) are equal in magnitude but opposite in phase.
- The current through the resistor (I_R) is in phase with the applied voltage (V).
- Since I_L and I_C are equal and opposite, they effectively cancel each other out at resonance.
- The net current (I) in the circuit is the same as the current through the resistor (I_R) because the effects of I_L and I_C cancel each other out.
- Therefore, the net current is in phase with the applied voltage.
- Since the net current (I) is in phase with the applied voltage (V), the phase difference between the applied voltage and the current flowing through the circuit at resonance is:
Phase Difference=0∘
At resonance in an LCR series circuit, the phase difference between the applied voltage and the current flowing through the circuit is 0 degrees.
Topper's Solved these Questions
- AC CIRCUITSBOOK - FIITJEECHAPTER - AC CIRCUITSEXERCISE - ASSIGNMENT PROBLEMS(OBJECTIVE Level - Il)
1 Video
- AC CIRCUITSBOOK - FIITJEECHAPTER - AC CIRCUITSEXERCISE - ASSIGNMENT PROBLEMS(OBJECTIVELevel - Il)
14 Videos
- AC CIRCUITSBOOK - FIITJEECHAPTER - AC CIRCUITSEXERCISE - ASSIGNMENT PROBLEMS (SUBJECTIVE)(leve II)
15 Videos
- COLLISION BOOK - FIITJEECHAPTER - COLLISION EXERCISE - (NUMERICAL BASED QUESTIONS)
4 Videos
Similar Questions
(a) An AC source of voltage V=V0sinωt is connected across a series combination of an inductor a capacitor and a resistor . Use the phasor diagram to obtain the expression for the impedance of the circuit and phase angle between the voltage and the current.
(b) A capacitor of unknown capacitance a resistor of 100 Ω and an inductor of self - inductance L =(4/π2) henry are in series connected to an AC source of 200 V and 50 Hz . Calculate the value of the capacitance and the current that flows in the circuit when the current is in phase with the voltage .
View SolutionA series L-C-R circuit is given in figure . The current through the circuit is
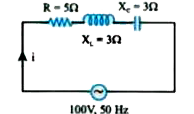
View Solution
Knowledge Check
An LCR circuit is connected to a source of alternating current. At resonance, the applied voltage and the current flowing through the circuit will have a phase difference of
Aπ/4BzeroCπDπ/2An L-C-R series circuit , connected to a source E, is at resonance. Then,
Athe voltage across R is zeroBthe voltage across R equals applied voltageCthe volatage across C is zeroDthe voltage across C equals applied voltageAn L-C-R circuit is connected to a source of A.C. current. At resonance, the phase difference between the applied voltage and the current in the circuit, is
AπBZeroCπ4Dπ2
In a LCR series circuit, if the phase difference between applied voltage and current is zero then
View SolutionIn a series L, R, C, circuit which is connected to a.c. source. When resonance is obtained then net impedance Z will be
View SolutionIn an L-C-R series, AC circuit at resonance
View SolutionThe phase difference between voltage and current in series L-C circuit is
View SolutionSeries LCR circuit is connected to an AC source of angular frequency ω. Current flowing in the circuit is found to lead the voltage by π/4. Magnitude of capacitance is
View Solution

