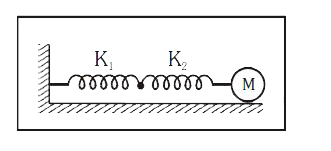
Two springs, of force constants k1 and k2, are connected to a mass maas shown. The frequency of oscillation of mass is f. If both k1 and k2 are made four times their original values, the frequency of oscillation becomes

f/2
f/4
4f
2f
The correct Answer is:D
f=12π√k1+k2m,fmax=12π√4k1+4k2m=2f.
Topper's Solved these Questions
- SIMPLE HARMONIC MOTION Book:RESONANCEChapter:SIMPLE HARMONIC MOTION Exercise:Advanced Level Problems
Explore 13 Videos
- SIMPLE HARMONIC MOTION Book:RESONANCEChapter:SIMPLE HARMONIC MOTION Exercise:Exercise- 3, PART - I
Explore 20 Videos
- SEMICONDUCTORSBook:RESONANCEChapter:SEMICONDUCTORSExercise:Exercise 3
Explore 88 Videos
- TEST PAPERSBook:RESONANCEChapter:TEST PAPERSExercise:FST-3
Explore 30 Videos
Similar Questions
What would be the period of the free oscillations of the system shown here if mass M1 is pulled down a little force constant of the spring is k, mass of fixed pulley is negligible and movable pulley is smooth
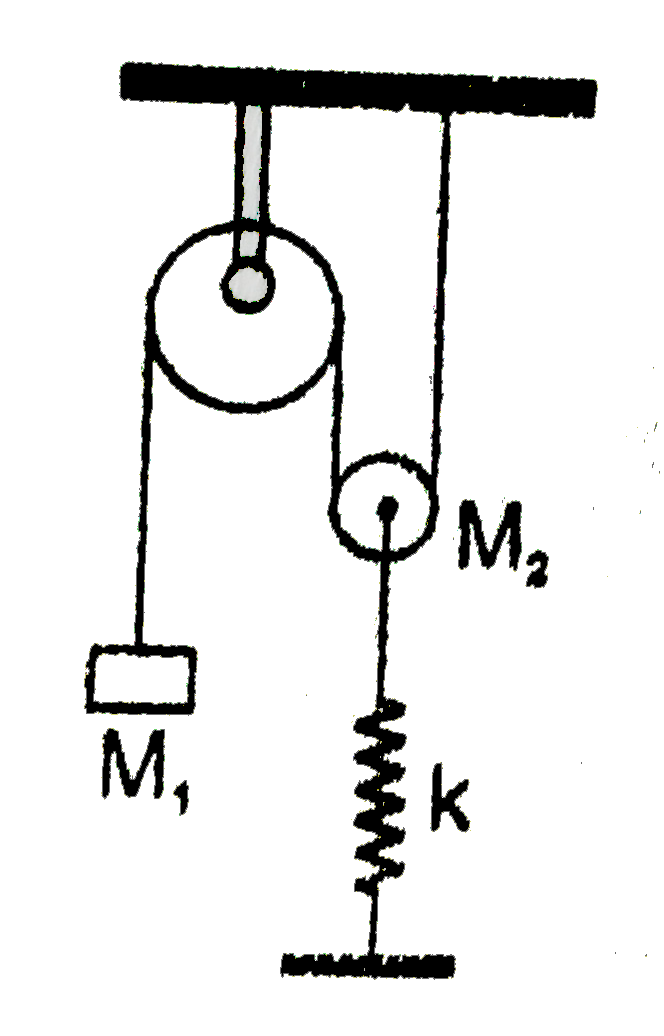
View SolutionA simple pendulum has time period (T_1). The point of suspension is now moved upward according to the relation y=Kt2,(K=1m/s2) where (y) is the vertical displacement. The time period now becomes (T_2). The ratio of T21T22 is (g=10m/s2).
View SolutionWhen p−n junction diode is forward biased then
View SolutionWhat will be the volume strength of 100 ml of H2O2 required to react completely with 61 ml of KMnO4 in acidic medium ? ( Given that 61l of KMnO4 reacts completely with 5 ml of 1M of K4[Fe(CN)6] where it converts into K+,Fe3+,CO2−3 and NO−3 )
View SolutionIn the arrangement shown in figure, pulleys are light and spring are ideal. K_(1) , k_(2) , k_(3) and k_(4) are force constant of the spring. Calculate period of small vertical oscillations of block of mass m .
View SolutionTwo springs are jonied and connected to a mass m as shown in figure. If the force constants of the two springs are k_(1) and k_(2) , shown that frequency of oscillation of mass m is
View SolutionAs shown in the figure, two light springs of force constant k1 and k2 oscillate a block of mass m. Its effective force constant will be

View SolutionTwo springs of force constants k_(1) and k_(2) , are connected to a mass m as shown. The frequency of oscillation of the mass is f . If both k_(1) and k_(2) are made four times their original values, the frequency of oscillation becomes
View SolutionTwo springs of force constants K_(1) " and " K_(2) are connected to a mass m as shown I the figure. If both K_(1) " and " K_(2) are made four times their original values, the frequency of oscillation becomes,
View SolutionA block of mass m is connected between two springs (constants K1 and K2) as shown in the figure and is made to oscillate, the frequency of oscillation of the system shall be-

View Solutionबल नियतांक K1 व kK2 वाली दो स्प्रिंगें एक द्रव्यमान m से चित्र 15.56 के अनुसार बँधी हैं | द्रव्यमान की दोलन आवृत्ति है | यदि K1 व rK2 के मान प्रारम्भ के चार गुने कर दिए जाएँ तो दोलन आवृत्ति हो जाएगी :

View SolutionIf T1andT2 are the time of oscillations for two springs of constants k1andk2 connected to the mass m individually then calculate the time period of oscillations when both the spring are connected to the same mass and subjected to oscillations.
View SolutionA block of mass M is placed on a smooth table. Its two sides are attached to fixed walls by means of collinear horizontal springs of spring constants k_(1) and k_(2)(k_(1)gt k_(2)) as shown in the Figure. The block is made to oscillate horizontally along the line of the two springs. The frequency of its oscillation is :
View SolutionTwo spring of spring constants k_(1) and k_(2) ar joined and are connected to a mass m as shown in the figure. Calculate the frequency of oscillation of mass m.
View Solutionदो हल्की स्प्रिंग जिनके बल नियतांक K1 तथा K2 हैं, M द्रव्यमान के गुटके को दोलित करती है, तो इसका प्रभावी बल नियतांक होगाः
View Solution
