दिखाइए कि परवलय y2=4ax की, प्रवणता 2 वाली जीवा को आन्तरिक रूप से 1:2 के अनुपात में बाँटने वाले बिन्दु का बिन्दुपथ एक परवलय है। इस परवलय का शीर्ष ज्ञात कीजिए।
The correct Answer is:(29,89)
माना A(t21,2t1) और B(t22,2t2) परवलय y2=4x की प्रवणताह वाली जीवा के अनंत बिंदु है
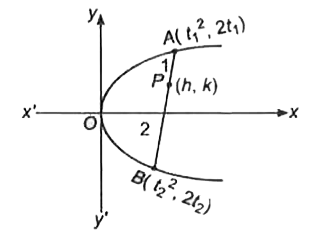
AB की प्रवणता =2t2−2t1t22−t21
=2t2−t1(t2−t1)(t2+t1)=2t2+t1
परन्तु m=2 (दिया है)
⇒2=2t2+t1
⇒t1+t2=1..........(i)
माना P(h,k), AB पर कोई बिंदु है जो AB को 1:2 के अनुपात में अंत: विभाजित करता है तब
h=2t21+t222+1 और k=2(2t1)+2t22+1
⇒3h=2h21+t22....(i)
तथा 3k=4t1=2t2....(iii)
समी (i) से t1 का मान समी (iii) में रखने पर, 3k=4(1−t2)+2t2
⇒3k=4−2t2⇒2t2=4−3k
⇒t2=2−3k2........(iv)
t1=1−t2 को समी (ii) में प्रतिस्थापित करने पर,
3h=2(1−t2)2+t22
⇒3h=2(1−2t2+t22)+t22
⇒3h=3t22−4t2+2
⇒3hg=3(t22−43t2+23)
⇒3h=3[(t2−23)2+23−49)]
⇒3h=3(t2−23)2+23
⇒3h−23=3(t2−23)2
⇒3(h−29)=3[2−3k2−23]2
⇒3(h−29)=3[43−3k2]2
⇒(h−29)=(43−3k2)2
⇒(h−29)=94(k−89)2
⇒(k−89)2=49(h−29)
अंत: अभीष्ट बिन्दुपथ (y−89)2=49(x−29)
यह एक परवलय निरूपित करता है जिसका शीर्ष (29,89) है
Similar Questions
माना कि परवलय x2=8y का शीर्ष O तथा उस पर बिंदु Q है। यदि बिंदु P रेखाखण्ड OQ को 1:3 के आन्तरिक अनुपात में विभाजित करता है, तो P का बिन्दुपथ है :
View Solutionपरवलय y2=8x एवं रेखा y=2x के मध्य स्थित क्षेत्र का क्षेत्रफल ज्ञात कीजिए।
View Solutionयदि एक त्रिभुज , जिसका एक शीर्ष परवलय के शीर्ष परवलय y2+4(x−a2)=0 तथा अन्य दोनों शीर्ष y-अक्ष तथा परवलय के प्रतिच्छेदन बिंदुओं पर हैं , का क्षेत्रफल 250 वर्ग इकाई है , तो 'a' का एक मान है
View Solutionमाना P(4,−4) तथा Q(9,6) परवलय पर स्थित दो बिन्दु है । O इस परवलय का शीर्ष बिन्दु है तथा X इस परवलय की चाप POQ का कोई ऐसा बिन्दु है, जिसके लिए का ΔPXQ क्षेत्रफल है, तो यह अधिकतम क्षेत्रफल (वर्ग इकाइयो में) है
View Solutionपरवलय y2=2x की स्पर्श रेखा 18x-6y+1= 0 का स्पर्श बिन्दु है
View Solutionपरवलय y2=4ax की, उन जीवाओं के मध्य बिन्दुओं का बिन्दुपथ जो मूल बिन्दु से होकर जाती हैं, होगा
View Solutionपरवलय y2=6x के उन बिन्दुओं को जिनकी भुज 24 है, शीर्ष से मिलाने वाली रेखाओं का समीकरण है
View Solutionपरवलय y2=4ax के बिन्दु (a4,a) पर अभिलम्ब का समीकरण है
View Solution

