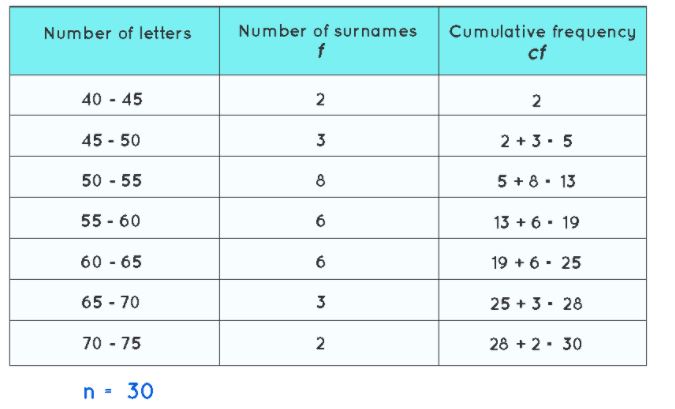
The distribution below gives the weights of 30 students of a class. Find the median weight of the students.
Here, n=30⇒n2=15
From the table, it can be observed that cumulative frequency (cf) just greater than 15 is 19, belonging to class 55 - 60.
Therefore, median class = 55−60
Class size, h=5
Lower limit of median class, l=55
Frequency of median class,f=6
Cumulative frequency of class preceding median class, cf=13
Median =l+[n2−cff]×h
=55+[15−136]×5
=55+(26)×5
=55+53
=55+1.67
=56.67
Therefore, median weight is 56.67 kg.
Similar Questions
The distribution below gives the weight of 30 students in a class. Find the median weight of students: Weight (in kg): 40-45 45-50 50-55 55-60 60-65 65-70 70-75 No. of students: 2 3 8 6 6 3 2
View SolutionThe distribution given below show the marks of 100 students of a class:
then find Ogive medium of data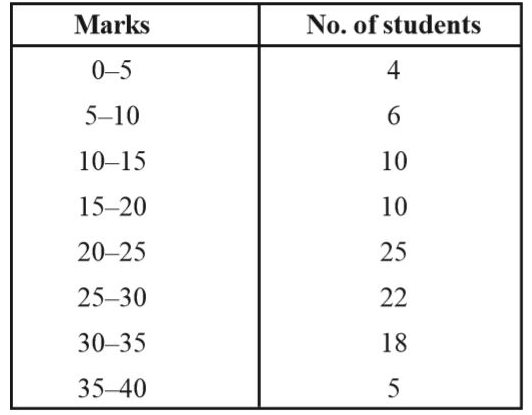
View Solution
Knowledge Check
Consider the following frequency distribution of the height of 60 students of a class:
The upper limit of the median class in the given data is:
 A165B155C160D170
A165B155C160D170
The weight (in kg) of students are given below :

Find the median weight of a student.
View SolutionFollowing table shows the weights of 12 students: Find the mean weight.
View SolutionFollowing frequency distribution gives the weights of 38 students of a class :
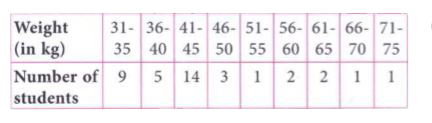
Based on the above information, answer the following questions.
Define an event whose probability is 1.
View SolutionFollowing is the data showing weights of 40 students in a class . Find its median .
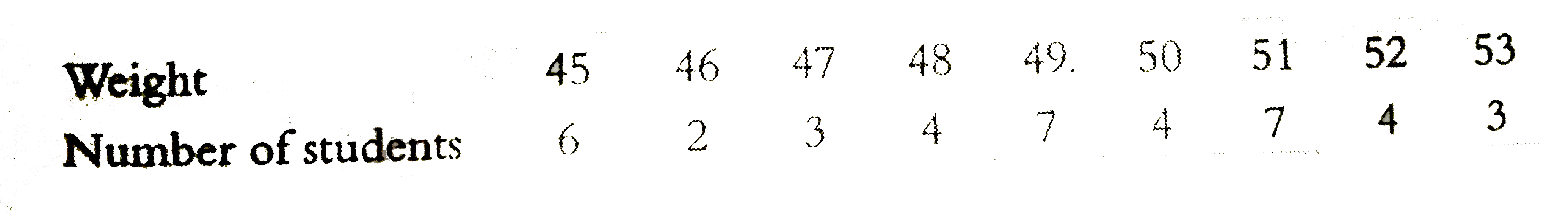
View SolutionFind the mean weight of 20 students in your class.
View SolutionFollowing frequency distribution gives the weights of 40 students of a class .

A student from the class is chosen at random . What is the probability that the weight of the chosen student is
(i) at most 60 kg (ii) at least 56 kg (iii) not more than 50 kg ?
View SolutionThe mean weight of 20 students is 25 kg and the mean weight of another 10 students in 40 kg . Find the mean weight of the 30 students .
View Solution