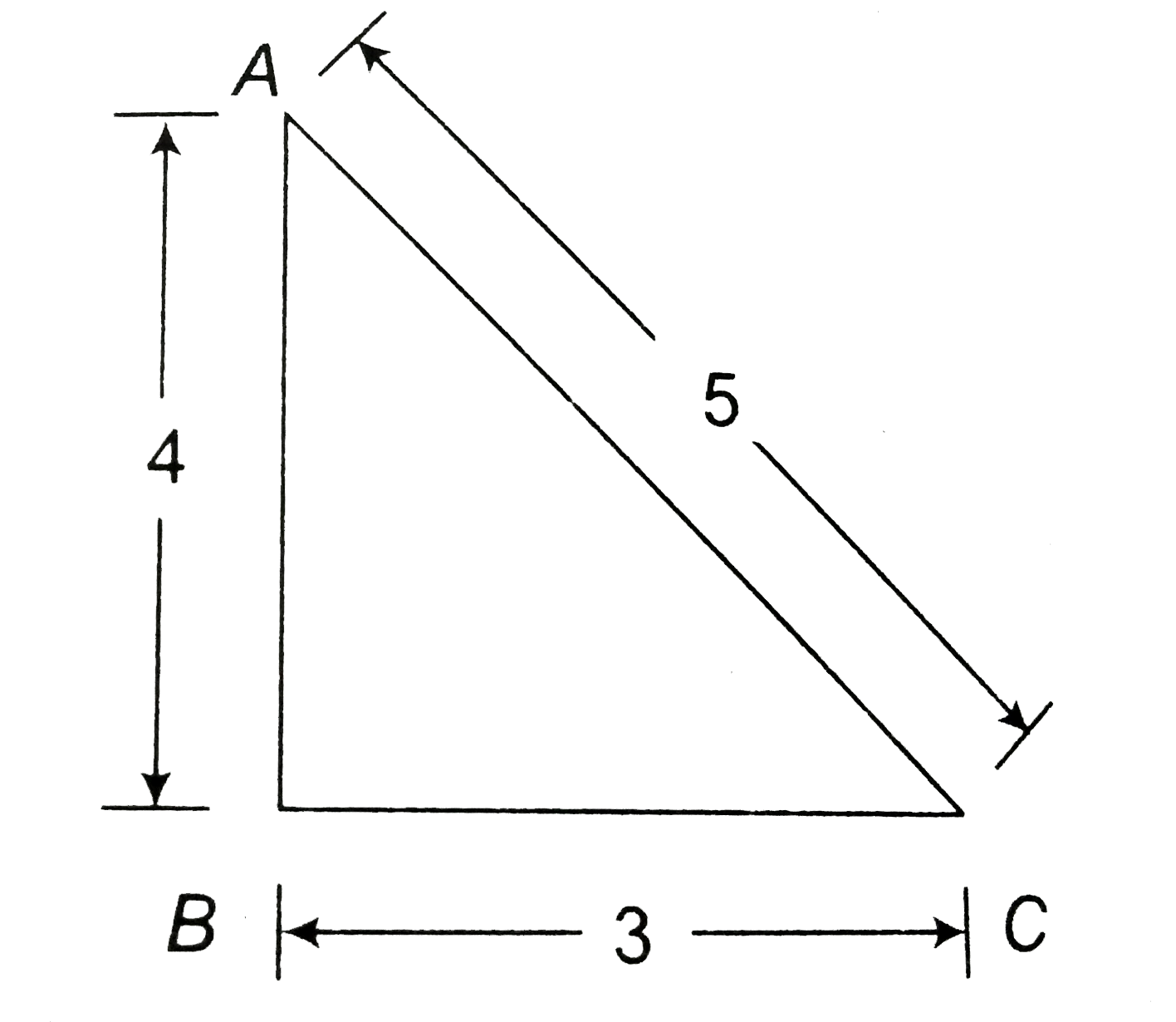
If in the figure AB=4,BC=6,CA=8 then AZ+BX+CY is:-

A
18
B
9
C
6
D
12
Video Solution
Text Solution
The correct Answer is:B
|
Answer
Step by step video, text & image solution for If in the figure AB = 4, BC = 6, CA = 8 then AZ +BX +CY is:- by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- RACEBOOK - ALLENCHAPTER - RACEEXERCISE - RACE 4
10 Videos
- RACEBOOK - ALLENCHAPTER - RACEEXERCISE - RACE 5
10 Videos
- RACEBOOK - ALLENCHAPTER - RACEEXERCISE - RACE 2
10 Videos
- LOGARITHMSBOOK - ALLENCHAPTER - LOGARITHMSEXERCISE - All Questions
107 Videos
- SEQUENCE AND PROGRESSIONBOOK - ALLENCHAPTER - SEQUENCE AND PROGRESSIONEXERCISE - Exercise (JA)
12 Videos
Similar Questions
Knowledge Check
The ABC is a triangular plate of uniform thickness. The sides are in the ratio shown in the figure. IAB,IBC and lCA are the moments of inertia of the plate about AB, BC and CA respectively. Which one of the following relation is correct?
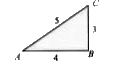 AIAB+IBC=ICABICA is maximumCIAB>IBCDIBC>IAB
AIAB+IBC=ICABICA is maximumCIAB>IBCDIBC>IABABC is a triangular plate of uniform A thickness. The sides are in the ratio shown in the figure. IAB,IBC,ICA are the moments of inertia of the plated about AB,BC and CA respectively. Which one of the following relation is correct?
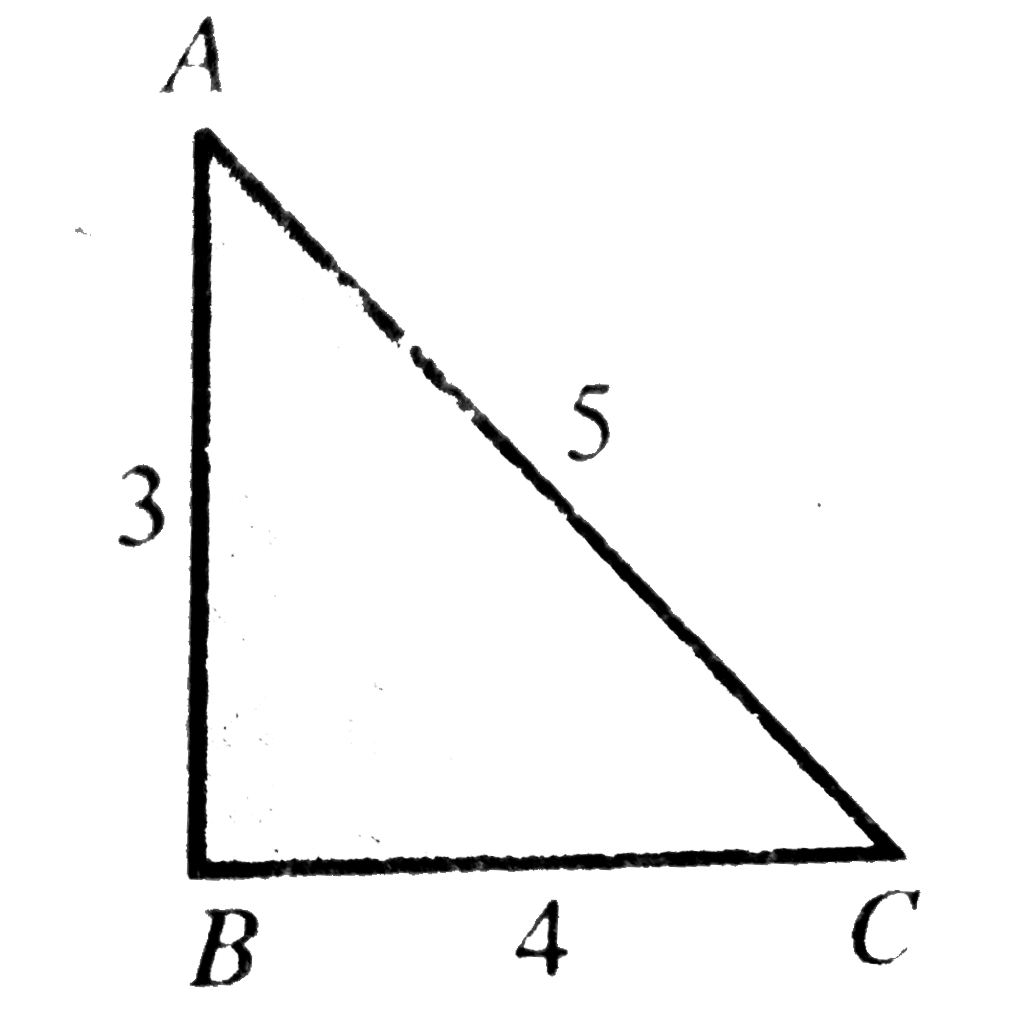 AICA is maximumBIAB>IBCCIBC>IABDIAB+IBC=ICA
AICA is maximumBIAB>IBCCIBC>IABDIAB+IBC=ICAABC is a traiangular plate of uniform thickness. The sides are in the ratio shown in the figure. IAB, IBC and ICA are the moments of inertia of the plate about AB, BC and CA repectively. Which one of the following relations is correct?
 AICA is maximumBIAB>IBCCIBC>IABDIAB+IBC=ICA
AICA is maximumBIAB>IBCCIBC>IABDIAB+IBC=ICA
In the figure 8.31, AX=AB=BXandAC=CY=YA. If CX=12cm, find BY.
View SolutionIn the adjoining figure, AB=8cm,DM=6cmandBC=6cm. Find the length of DN

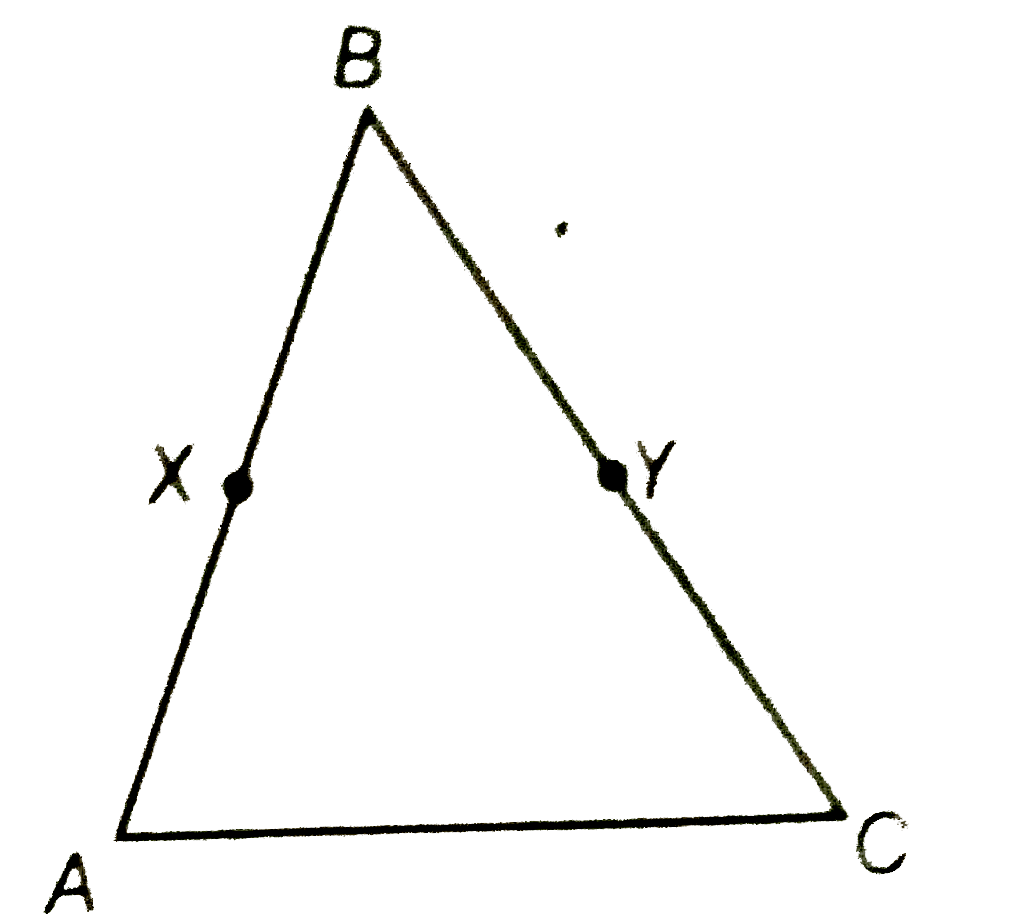
View SolutionIn the adjoining figure, if AB = BC and BX =BY, then show that AX=CY
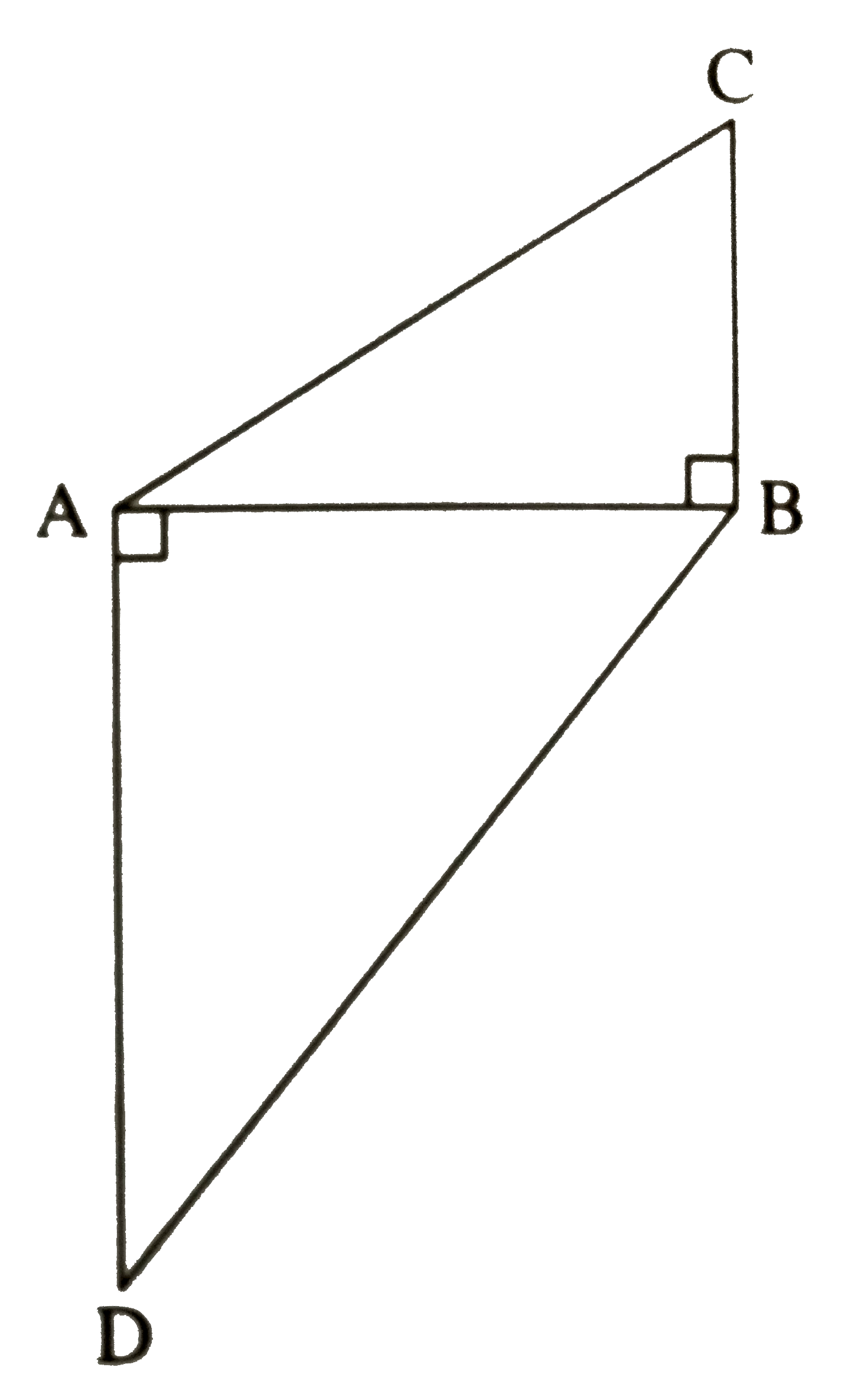
View SolutionIn the figure BC⊥AB,AD⊥AB,BC=4,AD=8, then find A(ΔABC)A(ΔADB).
View SolutionIf the lengths of the sides AB, BC and CA of a triangle ABC are 10 cm, 8 cm and 6 cm respectively and if M is the mid-point of BC and MN || AB to cut AC at N, then the area of the trapezium ABMN is equal to
View Solution