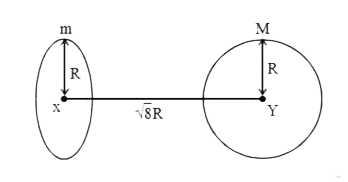
The centres of a ring of mass m and a sphere of mass M of equal radius R, are at a distance √8 R apart as shwon in fig. The force of attraction between the ring and the sphere is

2√227GmMR2
GmM8R2
GmM9R2
√29GmM9R2
The correct Answer is:A
Force on the sphere due to ring
F=ME here E=Gmx(x2+R2)3/2 where x=√8R
Topper's Solved these Questions
Similar Questions
The earth is assumed to be a sphere of raduis R. A plateform is arranged at a height R from the surface of the fve, where ve is its escape velocity form the surface of the earth. The value of f is
View SolutionIn the adjacent figure, x-axis has been taken down the inclined plane. The coefficient of friction varies with x as μ=kx, where k=tanθ. A block is released at O.
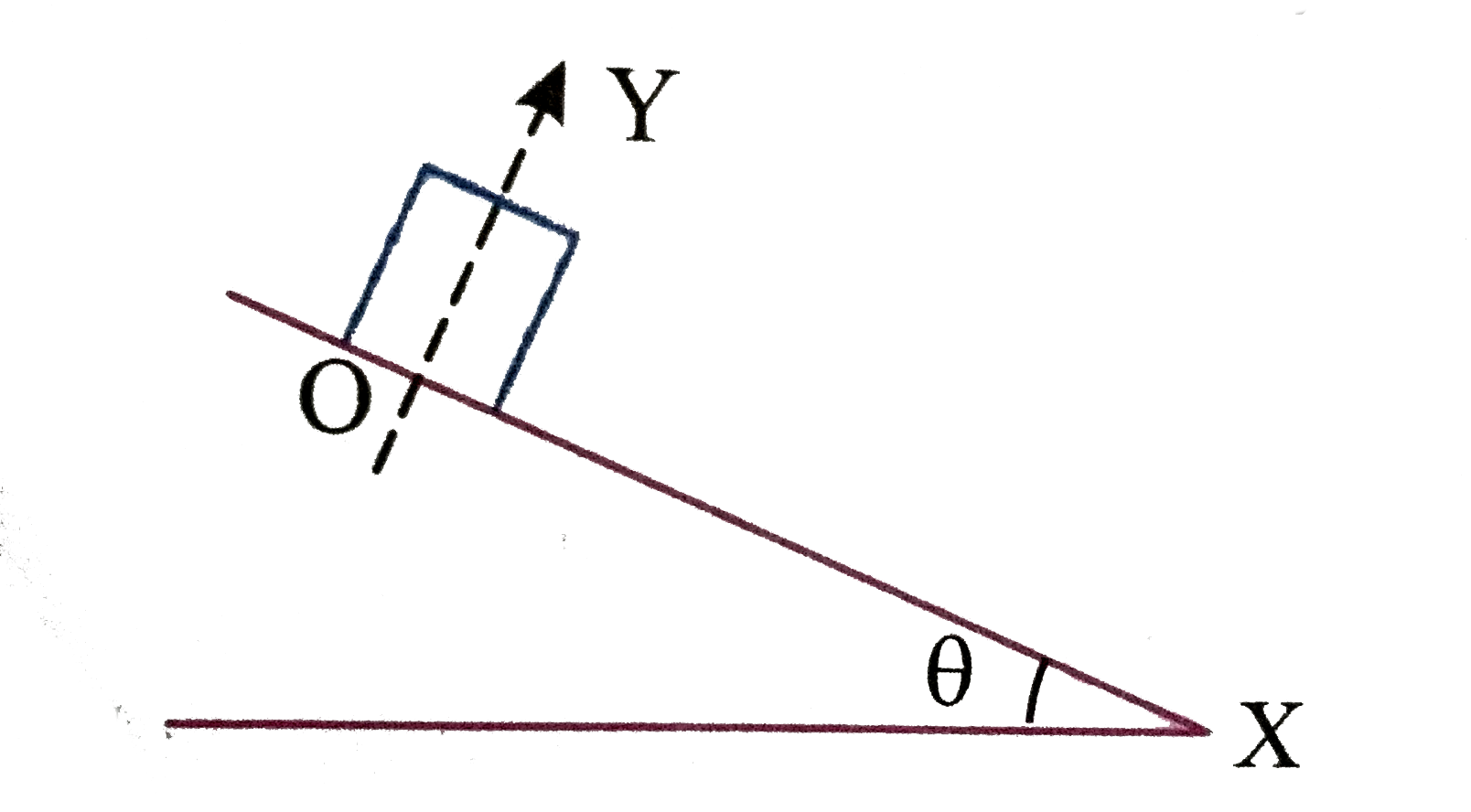
The maximum velocity of block will be:
View SolutionAn ice block is projected vertically up with a velocity 20 ms−1. The amount of ice that melt when it reaches the ground and if the loss of P.E. is converted into heat energy if the mass of ice block is 4.2 kg
View SolutionA uniform ring of mass m is lying at a distance sqrt(3) a from the centre of mass M just over the sphere (where a is the radius of the ring as well as that of the sphere). Find the magnitude of gravitational force between them .
View SolutionThe centres of a ring of mass m and a sphere of mass M of equal radius R , are at a distance sqrt(8) R apart as shown. The force of attraction between the ring and the sphere is
View SolutionAn unchanged conducting sphere of radius R is placed near a uniformly charge ring of radius R. Total charge on ring is Q. The centre of sphere lies on axis of ring and distance of centre of sphere from centre of ring is R
View SolutionA uniform ring of mass M and radius R is placed directly above a uniform sphere of mass 8M and of same radius R. The centre of the ring is at a distance of d=√3R from the centre of the sphere. The gravitational attraction between the sphere and the ring is
View SolutionA uiform ring of mass M and radius R is placed directly above a uniform sphere of mass 8M and same radius R. The centre of the sphere. The gravitational atraction between the sphere and the ring is
View SolutionA uniform ring of mass m and radius 3a is kept above a sphere of mass M and radius 3a at a distance of 4a (as shown in figure) such that line joining the centres of ring and sphere is perpendicular to the plane of the ring. Find the force of gravitational attraction between the ring and the sphere.
View SolutionA uniform ring of mass M and radius R is placed directly above a uniform sphere of mass 8 m and same radius R. The centre of ring is at a distance of d= sqrt(3)R from the centre of sphere. The gravitational attraction between the sphere and ring is
View SolutionA uniform ring of mas m and radius a is placed directly above a uniform sphere of mass M and of equal radius. The center of the ring is at a distance √3a from the center of the sphere. Find the gravitational force exerted by the sphere on the ring.
View SolutionA uniform ring of mass m and radius a is placed directly above a uniform sphere of mass M and of equal radius. The centre of the ring is at distance √3a from the centre of the sphere. Find the gravitational force exerted by the sphere on the ring.
View SolutionFind the force of attraction between a solid sphere of mass M and a ring of mass m as shown.
View SolutionFind the gravitational force of attraction between the ring and sphere as shown in the diagram, where the plane of the ring is perpendicular to the line joining the centres. If √8R is the distance between the centres of a ring (of mass 'm') and a sphere (mass "M") where both have equal radius "R'
View Solutionएकसमान वलय जिसका द्रव्यमान M तथा त्रिज्या R है, 8M द्रव्यमान व R त्रिज्या वाले गोले के ऊपर रखी है। वलय का केन्द्र, गोले के केन्द्र से d=√3R दूरी पर है। वलय तथा गोले के बीच गुरुत्वीय आकर्षण है
View SolutionA uniform ring of mass m is lying at a distance sqrt(3) a from the centre of mass M just over the sphere (where a is the radius of the ring as well as that of the sphere). Find the magnitude of gravitational force between them .
View Solution

