Consider a pair of perpendicular straight lines ax2+3xy−2y2−5x+5y+c=0.
Distance between the orthocenter and the circumcenter of triangle ABC is
4
9/2
8/3
7/4
The correct Answer is:4
As the lines are perpendicular, Coefficient of x2+ Coefficient of y2=0
∴a−2=0
or a=2
Also , abc+2fgh−af2−bg2−ch2=0
∴c=−3
Hence , the given pair of lines is
2x2+3xy−2y2−5x+5y−3=0
Factorizing , we get lines
x+2y−3=0and2x−y+1=0
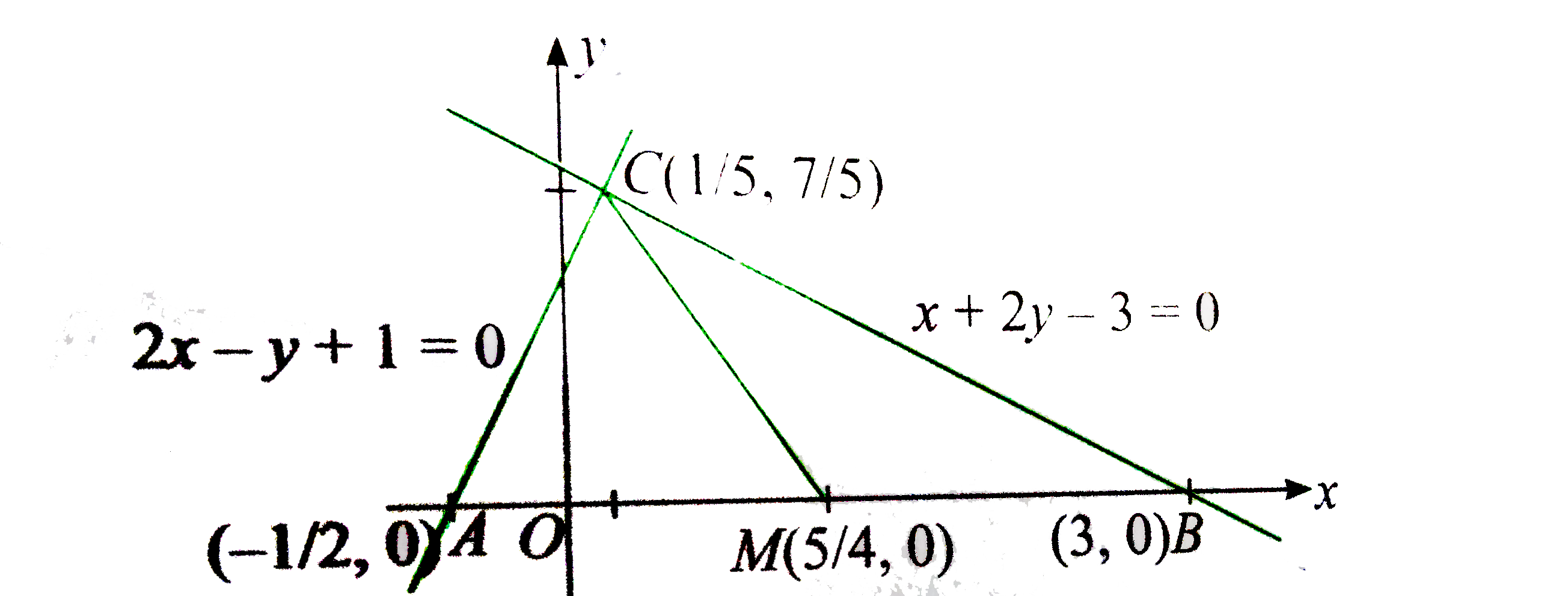
The point of intersection of the lines is C (1/5,7/5).
The points of intersection of the lines with the x- axis are A(3,0) and B (−1/2,0).
The orthocenter of triangle is C (1/5,7/5) and the circumcenter is the midpoint of AB which is M (5/4,0). Therefore,
CM√(54−15)2+4925=74
Topper's Solved these Questions
- PAIR OF STRAIGHT LINESBOOK - CENGAGECHAPTER - PAIR OF STRAIGHT LINESEXERCISE - Exercise (Numerical)
5 Videos
- PAIR OF STRAIGHT LINESBOOK - CENGAGECHAPTER - PAIR OF STRAIGHT LINESEXERCISE - Exercise (Multiple)
9 Videos
- MONOTONOCITY AND NAXINA-MINIMA OF FUNCTIONSBOOK - CENGAGECHAPTER - MONOTONOCITY AND NAXINA-MINIMA OF FUNCTIONSEXERCISE - Comprehension Type
6 Videos
- PARABOLABOOK - CENGAGECHAPTER - PARABOLAEXERCISE - Question Bank
21 Videos
Similar Questions
Knowledge Check
Consider a pair of perpendicular straight lines ax2+3xy−2y2−5x+5y+c=0.
The value of c isA-3B3C-1D1Consider a pair of perpendicular straight lines ax2+3xy−2y2−5x+5y+c=0.
The value of a isA1B3C2D-2Consider a pair of perpendicular straight lines 2x2+3xy+by2−11x+13y+c=0 The value fo c is
A-2B2C-3D3
Consider a pair of perpendicular straight lines 2x2+3xy+by2−11x+13y+c=0 The value fo c is
View SolutionConsider a triangle PQR with coordinates of its vertices as P(-8,5), Q(-15, -19), and R (1, -7). The bisector of the interior angle of P has the equation which can be written in the form ax+2y+c=0.
The distance between the orthocenter and the circumcenter of triangle PQR is
View SolutionFind the angle between the pair of straight lines x2−3xy+2y2=0
View SolutionConsider a pair of perpendicular straight lines 2x2+3xy+by−11x+13y+c=0
The value of |b+2c|is
View SolutionConsider a triangle PQR with coordinates of its vertices as P(-8,5), Q(-15, -19), and R (1, -7). The bisector of the interior angle of P has the equation which can be written in the form ax+2y+c=0.
The distance between the orthocenter and the circumcenter of triangle PQR is
View Solution

