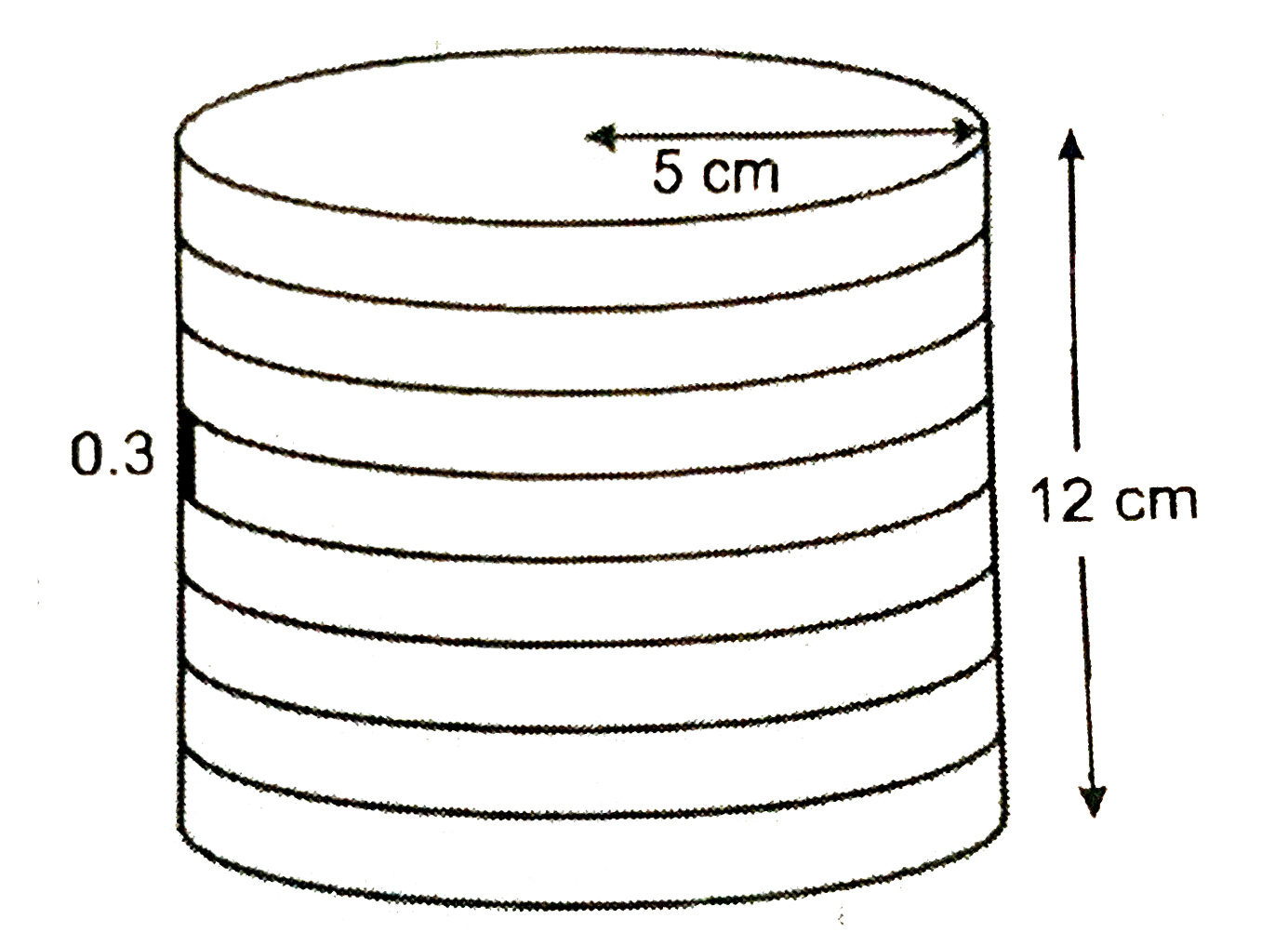
A wire of diameter 3mm is wounded around a cylinder whose height is 12 cm and radius 5 cm so as to cover the curved surface of the cylinder completely: find
(i) length of the wire.
(ii) mass of the wire assuming the density of copper to be 8.88 g per cm3
The correct Answer is:19093 cm3
(i) Let the wire wounded around the cylinder completes n revolutions.
Diameter (width) of wire = 3m=0.3 cm
So whole height of cylinder =0.3 n cm
But whole height of cylinder =12 cm
0.3 n=12→n=120.3=1203=40
So 40 revolutions are completed to wound the wire completely on the cylinder
In I revolution length of wire = 2 πr
In 40 revolutions length of wire =40×2πr
=80×227×5cm=1257.14cm
=12.57 m.(ii) Now radius of wire=0.32=0.15cm
volume of wire =area of cross section× length of wire
=π(0.15)2×1257.14=88.898cm3
Mass of wire = volume × density
=88.898×8.88 g=789.41 g
Hence length of wire = 12.57 m
and mass of wire =789.41 g
Similar Questions
A copper wire, 3 mm in diameter, is wound about a cylinder whose length is 12 cm, and diameter 10 cm, so as to cover the curved surface of the cylinder. Find the length and mass of the wire, assuming the density of copper to be 8.88gper cm3
View SolutionA copper wire 3 mm in diameter is rounded about a cylinder whose lengths is 1.2 m. and diameter is 10 cm., So as to cover the curved surface of the cylinder. The length of the wire is
View Solution
Knowledge Check
A rectangular paper 11 cm by 8 cm can be exactly wrapped to cover the curved surface of a cylinder of height 8 cm. the volume of the cylinder is
A66 cm3B77 cm3C88 cm3D121 cm3
Find the curved surface area of the cylinder whose height is 20 cm and the radius of base is 7 cm.
View SolutionA copper wire of diameter 6 mm is evenly wrapped on a cylinder of length 18 cm and diameter 49 cm to vover its whole surface. Find the length and the volume of the wire. If the density of copper be 8.8 g per cu-cm, find the weight of the wire.
View SolutionA copper wire of diameter 6mm is evenly wrapped on a cylinder of length 15cm and diameter 49cm to cover its whole surface. Find the length and volume of the wire. If the specific gravity of copper be 9g per cu cm, find the weight of the wire.
View Solutionradius and height of a cylinder are 10cm and 10.5cm respectivey Find the surface area of the cylinder.
View SolutionThe curved surface area of the cylinder is 1980 cm2 and the radius of its base is 15 cm. find the height of the cylinder .
View SolutionCurved surface area of a cylinder is 440cm2 and the radius of its base is 7 cm. Find the height of the cylinder.
View SolutionA copper wire of diameter 6 mm is evenly wrapped on a cylinder of length of length 15 cm and diameter 49 cm to cover its volume surface. Find the length and volume of wire. If the specific gravity of copper be 9g per cubic cm. Find the weigth of the wire.
View Solution
